位勢論

　　位勢的概念來源於物理學中的萬有引力理論。因為位勢在不分佈品質的地方是調和的，所以關於狄利克雷問題的研究一直是位勢論中的一個重要內容。由於（G.F.）B.黎曼把位元勢論和函數論統一處理，以及現代分析的基礎理論（如泛函分析、測度論、廣義函數、拓撲學等）在位勢論中的深入應用，位勢論成瞭數學領域內比較徹底地完成瞭現代化變革的一個分支。它同黎曼曲面論、偏微分方程、調和分析、概率論等數學分支也有著緊密的聯繫。

　　基本概念和主要原理　設Ω是n維(n≥2)歐幾裡得空間Rⁿ中的一個區域，μ是拉東測度(以下簡稱測度，若μ是非負的，也用μ≥0表示)，它的支柱S(μ)⊂Ω，K(x，y)是定義在Ω×Ω上的廣義實值函數，那麼

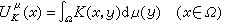稱為測度 μ的 K位勢。 K( x， y)則稱為位勢 U 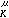( x)的核函數。

　　用|·|表示Rⁿ中的范數，當

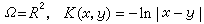時， U 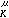( x)稱為平面上的對數位勢。當 Ω= R ⁿ( n≥3)，0＜α＜ n， K( x， y)=| x- y| 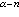時， U 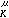( x)稱為 μ的α位勢（或裡斯位勢），此時也記作 U 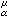( x)。特別α=2時， U 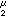( x)稱為 μ的牛頓位勢。下面限於討論 U 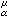扝∞的情形。

　　對Rⁿ裡的兩個測度μ和v，把

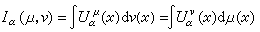稱為 μ， v的α相互能量。特別稱 I _α( μ)= I _α( μ， μ)為 μ的α能量。

　　把支柱包含在緊集K中且總質量等於1的非負測度全體記作

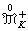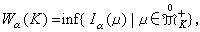，令 則

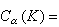
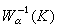稱為緊集 K的α容量。對任意集合 E，把

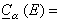
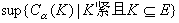稱為 E的α內容量，把

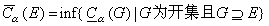稱為 E的α外容量。若 C _α( E)= c _α( E)，則說 E是α可定容的。G.紹凱證明瞭所有解析集，從而所有的波萊爾集是α可定容的。

　　當C_α(E)=0（或c_α(E)=0）時，稱E為α內（或外）零容集。一個性質若除瞭一個α內零容集外處處成立，則說該性質近乎處處成立；若除瞭一個α 外零容集外處處成立，則說該性質似乎處處成立。對任意零容的緊集K都有v(K)=0的測度v稱為C絕對連續測度。

　　集合E稱為α極集，若存在測度μ≥0，其α位勢在且僅在E上等於+∞。E是α極集的充要條件是：E為α零容的G_Λ集。

　　對緊集K，

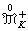關於渾收斂拓撲是緊的，從而存在 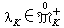使

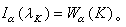
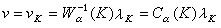稱為 K的α平衡測度，它滿足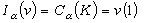： ( v(1)是 v的總質量)。它的位勢 Uǎ( x)稱為 K的α平衡位勢α它滿足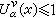： 在 S( v)處處成立而 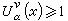在 K上近乎處處成立。特別當0＜α≤2時，由第一極大值原理知 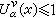在 R ⁿ處處成立。

　　對任意集E，當C_α(E)＜∞（或c_α(E)＜∞）時有相應的內(外)平衡測度。當0＜α≤2，α＜n，若E可定容且C_α(E)＜∞時，E的內、外平衡測度相等，稱之為E的平衡測度。此時v是滿足①支柱在E，②v(1)=C_α(E)，③在E上似乎處處有

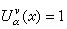諸條件的惟一測度。平衡測度是 C絕對連續的，而平衡位勢 Uǎ( x)是這樣一族α位勢 U 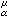( x)的下確界： μ≥0且 U 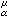( x)≥1在 E上似乎處處成立。因此，若 μ≥0且 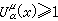在 E上似乎處處成立，則 μ的總質量 μ(1)≥ C _α( E)。

　　由於測度的α能量非負，所以能量有限的測度全體在通常的線性組合的意義下，以I_α(μ，v)為內積構成一個實的準希爾伯特空間ε_α，其中非負測度全體ε

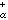是ε _α的一個完備凸錐。若 K緊，那麼支柱含於 K中的具有限α能量的非負測度全體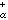ε ( K)是ε 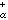的完備凸子錐，因此ε 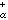的任何元素 μ在ε 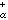( K)上有惟一的正交投影 β _K μ，即滿足

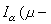
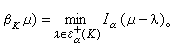當0＜α≤2時， β _K μ是掃除問題的解，即 β _K μ滿足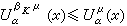： 在 R ⁿ處處成立且等號在 K上似乎處處成立。

　　若不假定μ≥0的能量有限，則存在惟一的支柱含於K的測度β_Kμ使得方程

對任意 λ∈ε 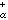成立且 β _K μ是掃除問題的解。

　　當0＜α≤2，α＜n時，對α容量有限的波萊爾集E及測度μ≥0，設A是E的緊子集全體以包含關系為序的有向集，則網{β_Kμ|K∈A}的渾極限β_Eμ存在，稱β_Eμ為μ到E的掃除測度，掃除測度β_Eμ是μ到E的掃除問題的解，且掃除位勢

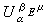是在 E上似乎處處滿足 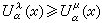的位勢族{ U 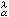( x)}的下確界函數。

　　設ε_x是在點x的狄喇克測度，則β_EεC稱為E的α格林測度。對任意測度μ，

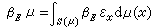。當 x ₀∈ E且 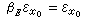時，稱 x ₀為 E的α正則點，當 x ₀∈ E而

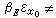
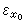時，稱 x ₀為 E的α非正則點。

　　開集Ω的邊界記作дΩ，餘集記作CΩ，稱

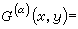
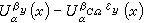為 Ω的α格林函數。以格林函數為核的位勢叫做格林位勢。當 α=2時，對任意的波萊爾集 E⊆д Ω，由 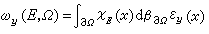定義的д Ω上的測度ω _y稱為關於 y的調和測度，其中 X _E表示 E的特征函數。

　　當2＜α＜n時，關於測度的掃除問題一般無解，但J.德尼利用廣義函數解決瞭這個問題。

　　用ε宎表示單位質量在以y為球心，r為半徑的球面的均勻分佈。若函數f在Ω裡下半連續且滿足

　　①

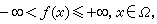
　　② 對任何x∈Ω，存在正數ρ使對任意正數r＜ρ有

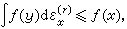則稱 f在 Ω裡超調和。不恒等於+∞的超調和函數稱為上調和函數。若- f上調和，就說 f下調和，既上調和又下調和的函數叫調和函數。

　　當2≤α＜n時，α位勢U

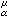( x)是上調和函數。裡斯分解定理指出： f在區域 Ω裡上調和的充要條件是存在惟一的 Ω上的測度 μ≥0，使得對任何相對緊的區域 Ω ₁⊂ Ω ₁⊂ Ω有

，

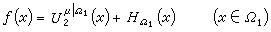這裡 μ| Ω ₁表示 μ在 Ω ₁的限制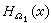， 在 Ω ₁裡調和。

　　當0＜α＜2時，α位勢不是上調和函數。但當U

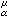( x)是 μ幾乎處處有限時，它是α上調和函數。一個函數稱為α上調和函數，指的是滿足下面條件的非負的不恒為+∞的下半連續函數：

　　①

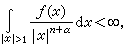
　　②

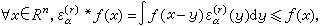式中

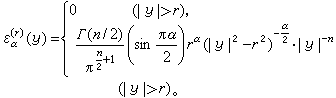
　　　如果在x₀的一個鄰域內連續的函數滿足條件①且對充分小的r恒有

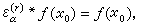則稱 f( x)在 x ₀是α調和的。若 f( x)在集 Ω上點點α調和，則稱 f在 Ω裡α調和。對於α上調和函數，同樣也有類似的裡斯分解定理。

　　對上調和函數的連續性的研究導致細拓撲概念的引入。為敘述方便，也稱上調和函數為2－上調和函數。用E′表示集E的極限點全體，若x₀∈E′或x₀∈E′且存在α上調和函數u(x)使

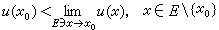成立，則稱 E在 x ₀是α瘦的。 E在 x ₀是α瘦的充要條件是 x ₀ ∈ E或 x ₀是 E的α非正則點。

　　若E的餘集在x₀為α瘦則說E在x₀是α肥的。若E在E的每一點都是α肥的，則說E是一個α肥集。α肥集全體構成Rⁿ裡一個拓撲，稱為α細拓撲。2-瘦和2-細拓撲通常分別稱為瘦和細拓撲。開集必為α肥集，α細拓撲比通常拓撲細。此外，當α＜α′時，α細拓撲嚴格細於α′細拓撲；α細拓撲是使所有α上調和函數（包括α位勢）都連續的最粗拓撲。在α細拓撲下的極限叫α細極限。對α細拓撲，α細極限與不相切極限的關系，J.L.杜佈等人曾有深入的研究。

　　第一極大值原理　當0＜α≤2，μ≥0時，若U

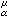( x)≤ M， μ幾乎處處成立，則該不等式處處成立。

　　當2＜α＜n時，第一極大值原理不成立。

　　廣義極大值原理　當0＜α＜n時，若U

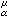( x)≤ M在 S( μ)上成立，則 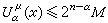處處成立。

　　第二極大值原理　又稱控制原理。設μ≥0是能量有限的測度，λ≥0是任意測度，若

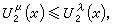μ幾乎處處成立，則該不等式處處成立。

　　當0＜α＜2時，若U

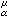( x)關於 μ≥0幾乎處處有限， f( x)是α上調和函數，且 U 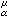( x)≤ f( x)， μ幾乎處處成立，則該不等式處處成立。

　　惟一性原理　設0＜α＜n，μ₁，μ₂是絕對連續的非負測度，若

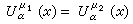在 S( μ ₁)∪ S( μ ₂)上似乎處處成立，則 μ ₁= μ ₂。

　　下包絡原理　設0＜α≤2，則對任意兩個非負測度μ，v存在測度λ，使

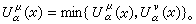
　　連續性原理　若把U

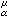( x)看作支柱 S( μ)上的函數時是取有限值的連續函數，那麼 U 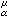( x)在整個空間上也連續。

　　能量原理　對任意測度μ，

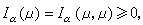等號成立當且僅當 μ=0。

　　掃除原理　當0＜α≤2時，對任意α容量有限的波萊爾集E和具有限位勢的測度μ≥0，掃除問題有解，即存在支柱在E的測度β_Eμ使在E上似乎處處有

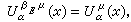且在 R ⁿ處處有 。

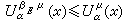　　狄利克雷問題　廣義形式可敘述為：若Rⁿ的區域Ω的邊界дΩ是緊的，對дΩ上的函數f，是否存在惟一的函數u在Ω裡調和且對每一個正則邊界點y滿足：

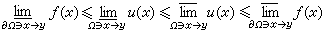且當 Ω是無界區域時，

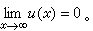
　　下面采用的佩隆方法是解這個問題的最有效工具，它是歷史上有名的施瓦茲交錯法及龐加萊掃除法的發展與精密化。

　　令

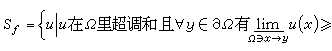
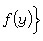（當 Ω無界時還要求 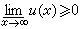），記

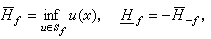那麼 H _f≤ H _f。當此式等號成立且僅取有限值時稱 f是可解的。 f可解的充要條件是對於每個 x∈ Ω， f關於д Ω的調和測度 ω _x可積分。這時 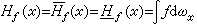就是所要求的惟一解。特別，若 f連續則必可解，而且， y∈д Ω為正則邊界點的充要條件是對 д Ω上的每個連續函數 f有 。

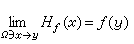　　在一定條件下，也可以考慮關於α調和函數的狄利克雷問題。

　　當0＜α≤2，α＜n時，y∈дΩ為α正則邊界點當且僅當Ω的餘集在y是α不瘦的。維納判別法指出，若0＜q＜1，令

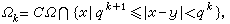則 y∈д Ω為α非正則的充要條件是 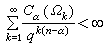，式中 C _α( Ω _k)表示 Ω _k的α容量。 Ω的α非正則邊界點全體是α零容集。此外，關於正則點的充要判別法還可利用閘函數、格林函數、平衡位勢等給出，而龐加萊錐判別法是常用的充分判別法。

　　狄利克雷原理　設D₀是Rⁿ的有界區域Ω上的連續可微且梯度平方可積的函數全體。在D₀定義內積＜

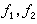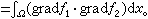＞ 記 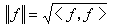，則依等價關系“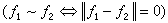～” 得到的商空間 D是準希爾伯特空間。若 f∈ D ₀且有界並可連續地開拓到 Ω，則狄利克雷問題的解 H _f滿足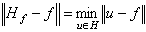： ，這裡 H表示 D ₀中的調和函數全體所組成的 D的子希爾伯特空間，即 H _f是 f在 H上的正交投影。

　　德尼用廣義函數證明，D的完備化是由下述BLD函數f組成的：f似乎處處有限且D₀中有子列似乎處處收斂於f。若f是有界區域Ω₁(ɔΩ)上的BLD函數，則在Ω上，H_f存在且除瞭一個附加常數外是惟一的使 ‖u-f‖達到極小的BLD函數，也是惟一的在Ω裡調和並且可由f開拓成Ω₁上的BLD函數的函數。

　　上述結果都可以推廣到ε空間的相對緊的子區域上去。

　　格林空間與格林函數　連通的豪斯多夫空間Ω若滿足下面條件則稱之為ε空間：Ω的每一點x有一個開鄰域V_x連同一個把V_x變Rⁿ上的一個開子集的同胚y

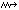M _x( y)，並且任何兩個這樣的鄰域 V C與 V _y的交 V C∩ V _y在相應的兩個同胚變換下是保距的（當 r≥3）或共形的(當 n＝2)。於是作為局部性概念的調和、超調和、上調和函數等可在ε空間 Ω上相應地定義。更一般地，也可以用 R ⁿ代替上述 R ⁿ來定義ε空間。這種廣義ε空間將有若幹無窮遠點。

　　若ε空間Ω上存在正的非常數的上調和函數，則稱Ω為格林空間。例如Rⁿ(n≥3)及Rⁿ的任何有界子區域都是格林空間，R²是ε空間而不是格林空間。格林空間Ω上必存在滿足下列條件的函數G_x(y)，稱之為以x∈Ω為極的格林函數：①G_x(y)>0；②在Ω\{x}上，G_x(y)調和；③存在x的鄰域V(⊂V_x)使得對每個y∈V，若記y′=M_x(y)，則

式中 K為α=2時的核函數， u 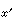調和。

　　由於G_x(y)=G_y(x)，故記作G(x，y)=G(y，x)。

　　稱

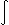G( x， y) d μ( x)( μ≥0)為格林位勢。它或恒為+∞，或是個以0為最大調和下屬的上調和函數。

　　最一般的抽象邊界與CC緊致化　在非空集合Ω上賦予拓撲τ，設I是任一非空號標集，若∀i∈I，Ω的開子集族B_i為Ω的濾基，則I可成為Ω的鑲上去的抽象邊界，因為在Ω∪I上存在滿足下述條件的拓撲τ₁：①Ω∈τ₁；②τ₁在Ω的誘導（相對）拓撲正好是τ；③每個i∈I的鄰域系與Ω的交構成由B_i生成的濾子。這樣的拓撲中最細者在I上誘導出離散拓撲；而最粗者當I是Ω上抽象調和函數凸錐的極端母線全體時就稱為極小細拓撲。

　　在實用中，常據在Ω上所考慮的函數族的性質來引入邊界且保證Ω鑲邊後是緊的。康斯坦丁斯庫－科尼緊致化定理即若Ω是非緊的局部緊的豪斯多夫空間，φ是一族從Ω到[-∞，+∞]的連續函數，則存在惟一（至多相差一個同胚）的緊空間輩滿足：①Ω在輩中是開的且在輩中稠密；②φ中每個函數f能開拓成輩上的連續函數箣；③箣全體能辨別理想邊界Δ=輩\Ω。

　　輩也可看成關於Ω上的這樣的一致結構的完備化空間：它是使得φ中每個函數都一致連續且相應的一致拓撲與Ω原有拓撲相容的最粗的一致結構。

　　作為應用，適當選取φ可以得到如下位勢論中常用的緊致化。

　　亞歷山德羅夫單點緊致化　這時φ為空集。

　　斯通－切赫緊致化　這時φ是Ω上的所有廣義實值連續函數。

　　凱雷克亞托－斯托伊洛夫緊致化　這時φ由這樣的實值連續函數f組成：在Ω中有緊子集K_f使得Ω\K_f是一些區域之並集且在每個區域上f取常數值。

　　羅伊登緊致化　這時Ω是ε空間，φ是所有實連續的BLD函數。

　　倉特善緊致化　這時Ω是ε空間，φ是滿足下述條件的實連續BLD函數f全體：Ω有閉子集F_f使得f在Ω\F_f裡調和且在那些於F_f上取值等於f的BLD函數中，f的狄利克雷積分（即‖f‖_D）達到最小。

　　馬丁緊致化　是位勢論中重要的一種緊致化。

　　馬丁空間與馬丁邊界　為紀念R.S.馬丁，將格林空間Ω相對於函數族

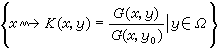（ y ₀∈ Ω任意取定）的CC緊致化空間輩 稱為馬丁空間； Δ＝輩\ Ω稱為馬丁邊界。所有函數 xм→ K( x， y)( y∈ Ω)，在輩都有連續的開拓且能辨別 Δ。輩可度量化。 R ⁿ的一般區域的歐氏邊界與 Δ全然不同；但當 Ω是球或其他較為正則的區域時，輩等同於 Ω的歐氏閉包；對 R ²的單連通格林區域， Δ等同於卡拉西奧多裡分歧邊界。

　　調和函數u＞0稱為極小調和函數，指的是任何不大於u的正調和函數必與u成比例。若u極小調和，必存在x∈Δ使得u(y)=u(y₀)·K(x，y)。稱這樣的X為Δ的極小點。極小點全體Δ₁是G_Λ集。對任一非負調和函數u必存在唯一的分佈在Δ₁上的拉東測度μ使得∀y∈Ω，

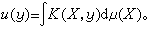稱此式為馬丁積分表現，其右端是雙層位勢的推廣。它促使瞭著名的關於凸錐的極端點的紹凱定理的產生並且後者反過來簡化瞭前者的證明。

　　對馬丁邊界同樣可考慮狄利克雷問題，可討論一個集在X∈Δ₁的瘦與肥並進而把Ω上的細拓撲開拓到Ω∪Δ₁。對任意上調和函數u＞0及調和函數h＞0，u/h在Δ₁上至多除去一個h零測集外處處有細極限，這是杜佈對著名的法圖定理即球內的正調和函數在邊界上幾乎處處有不相切極限的重大推廣。

　　馬丁緊致化有許多推廣的形式。例如，當考慮的函數族是由某一橢圓型方程（特別是Δu＝pu）在Ω上的格林函數G′(x，y)的商

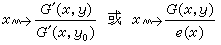（ e( x)為確定的有界正解）組成時，可得到橢圓馬丁邊界 Δ′，並進而可研究 Ω的橢圓維數，所考慮的方程的解空間的結構以及 Δ′與其他邊界的關系等。

　　馬丁邊界可翻譯成概率的語言並在隨機過程論中得到應用與推廣。

　　局部緊阿貝爾群上位勢論　由於拓撲學和代數學，特別是群上傅裡葉分析的發展，使這種群上的位勢論取得瞭豐富的成果。

　　設G是局部緊阿貝爾群，若對G上一個測度網(μ_α)_α∈A，存在一測度μ，使對任意f∈C_c。（支柱緊的連續函數全體），均有

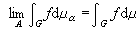，則稱( μ _α) _α∈A渾收斂於 μ。

　　若G上一正測度集合(μ_t)_t＞0，滿足以下條件：①μ_t(G)≤1，t＞0；②

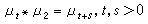，s>0；③ 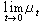渾收斂於狄喇克測度ε ₀；④渾積分 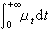存在，則稱( μ _t) _{t ＞0}是 G上一個遷移測度卷積半群。 K= 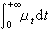稱為它所對應的位勢核。若測度

，

則測度 K* σ就稱為 K位勢。

　　一個正測度ξ稱為關於(μ_t)_t＞0是過度的，若對所有t＞0，ξ是μ_t上調和，即μ_t*ξ ≤ξ；一個正測度ξ 稱為關於(μ_t)_t＞0是不變的，若對所有t＞0，ξ是μ_t調和的，也就是μ_t*ξ=ξ。每一個K位勢必為過度測度;反之，每一個過度測度必是單調增加K位勢網的渾極限。對過度測度ξ，裡斯分解定理成立，也就是ξ=K*σ+η，σ∈D⁺(K)；η是不變測度。

　　若

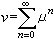，其中正測度 μ滿足 μ( G)≤1， μ ⁿ是 n重卷積， μ ⁰＝ε ₀則稱 v為基本核。若 K為位勢核，則 λ K+ε ₀， λ＞0，必為基本核。基本核對所有開集滿足掃除原理，所以位勢核 K對所有開集也滿足掃除原理。

　　若ω是開集，ξ是過度測度，測度

是過度測度，在 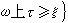稱為ξ在ω上的簡化測度。對簡化測度，裡斯分解定理仍成立。利用簡化測度可證明平衡分佈原理和正質量原理；也就是若 σ ₁， σ ₂∈ D ⁺（ K），且 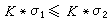，則有 σ ₁( G)≤ σ ₂( G)。在1978年，還證明瞭電容器原理，即若ω _G是 G上哈爾測度， Ω ₀， Ω ₁是一對開集 Ω ₀∩ Ω ₁=ø，且 Ω ₀是緊的，那麼存在正測度 μ ₀， μ ₁∈ D ⁺( K)，使得 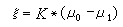滿足：①0≤ξ ≤ω _G；②ξ =ω _G在 Ω ₀；③ξ =0在 Ω ₁；④支柱

。

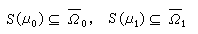關於位勢核 K在理想邊界的性質，能量有限復測度空間的完備化以及廣義函數的引入等，都有瞭一系列很好的結果。

　　如果把上述遷移測度卷積半群(μ_t)_t＞0所滿足的條件①、③放寬為

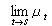渾收斂於 μ _s， t，s>0和 μ ₀= ε ₀，測度 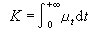就稱為亨特核。亨特核滿足掃除原理和推廣的電容器原理。

　　設x為局部緊豪斯多夫空間，ξ 為x上一個處處稠密正拉東測度（對任意非空開集ω，ξ(ω)>0），由x上一族局部ξ可積的復函數u(x)組成的希爾伯特空間D＝D(x，ξ)，若滿足下列三條公理：①對任一緊集K，存在一數A(K)>0，使得

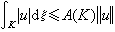；② C _c∩ D在 D中和 C _c中稠密；③對復平面上每一個正常收縮映射 T和任一 u∈ D，有 T u∈ D，且‖ T u‖≤‖ u‖，則稱 D( x，ξ)為ξ狄利克雷空間。若對 u∈ D，存在一拉東測度 μ，使得

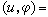
， φ∈ C _c∩ D，則稱 u為 μ的位勢。在ξ 狄利克雷空間中，也有相應的電容器原理、平衡分佈原理和掃除原理等。

　　公理化位勢論　由於位勢論的大部分結果都可由其狄利克雷問題、極值原理和收斂性質三個基本原理導出，且為瞭適應偏微分方程和隨機過程的需要，公理化位勢論，即調和空間理論迅速地發展起來，它提供瞭統一處理問題的方法。從50年代起，G.L.陶茨、杜佈和M.佈雷洛特等在這方面做瞭開創性的工作，C.康斯坦丁斯庫和A.科尼在70年代初期建立瞭一般調和空間理論。

　　一般公理系統　又稱康斯坦丁斯庫－科尼公理系統。在一個局部緊、第二可數的豪斯多夫空間X的每一開集U上，給出一個由一族不取值－∞的下半連續函數組成的凸錐U(U)，所有這些函數的全體構成x上的一個函數簇U。拓撲空間x上的函數簇是指定義在x的開集上滿足下列條件的一個映射U：①對於x的任意開集U，U(U)是U上的函數集；②對於X的任意開集U，V，U⊆V，若f∈U(V)，則f|_U∈U(U)；③對於x的任意開集族(U_α)_α∈A，一個

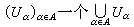上的函數 f，若對一切α ∈ A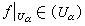， ，則 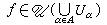。U稱為 x上的超調和簇，凸錐U( U)中的函數叫做 U上的超調和函數。超調和是局部性質。

　　在一個開集上，一個函數u稱為亞調和函數，如果-u是超調和的，若一個函數h既是超調和亦是亞調和，則說h是調和函數。

　　一個開集U稱為可解集，如果在U上超調和函數的極小值原理成立，並且每一f∈C_c(дU)在U內的廣義狄利克雷問題是可解的。f的解H

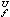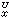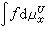在 U上可表示為調和測度 μ 的積分 ， μ 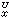分佈在д U上且大於等於零。

　　一般公理系統包括如下四個公理：

　　正(P)公理　x上的每一點都存在有該點的一個開鄰域上的一個調和函數，使它在該點取正值。

　　可解(R)公理　可解集全體構成拓撲空間x的一個拓撲基。

　　完備(C)公理　在一個開集U上，任一不取-∞的下半連續函數u若滿足在U的每一相對緊的可解子集V(V⊂U)上，

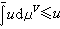，則 u∈U( U)。

　　鮑厄收斂(BC)性質　單調增加、局部一致有界的調和函數列的極限仍是調和函數。

　　滿足上述公理的有序偶(x，U)叫做調和空間（或叫CC調和空間）。

　　佈雷洛特公理系統　在一局部緊、第二可數的豪斯多夫空間x上一個調和函數簇H滿足如下公理。

　　① 每一開集U上的調和函數全體H(U)是C(U)的一個線性子空間。

　　② 正則區域構成x的一個拓撲基。

　　所謂正則區域即一個相對緊的區域V，其邊界дV上的每一連續函數都可惟一地開拓成為V上的調和函數H抦，並且當f≥0時H抦≥0。

　　③ 區域上的單調增加的調和函數列的極限是調和函數或恒等於+∞。

　　有序偶(x，H)叫做佈雷洛特調和空間，它是第一個完善的公理系統。佈雷洛特調和空間上的位勢論與經典位勢論最為接近。

　　此外，比較典型的還有鮑厄-博博克-康斯坦丁斯庫-科尼公理系統（簡稱BBCC公理系統）。二階橢圓型偏微分方程滿足佈雷洛特公理系統，但熱傳導方程卻不滿足佈雷洛特公理系統，而滿足BBCC公理系統。一個佈雷洛特調和空間是一個BBCC調和空間，而BBCC調和空間是一般的CC調和空間。佈雷洛特公理系統嚴格強於BBCC公理系統，而BBCC公理系統又嚴格強於一般公理系統。設U是調和空間(x，U)的開子集，u是U上超調和函數，若在U的每一相對緊的可解子集V(V⊂U)上，

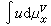是調和函數，則 u叫做上調和函數。- u叫做下調和函數。上、下調和函數在一個稠密集上取有限數值。以0為最大調和下屬的非負上調和函數叫做位勢。在調和空間中，相應的裡斯分解定理仍然成立。

　　對於佈雷洛特調和空間，R.M.埃爾韋證明瞭，在滿足一定條件下，若區域上存在正位勢，則格林函數也存在。一個佈雷洛特調和空間若存在一個相容的對稱格林函數系，稱為自共軛調和空間，其原型來自偏微分方程Δu=сu。F.Y.馬埃達通過引入梯度測度的概念，在自共軛調和空間上建立瞭廣義格林公式。

　　位勢論與概率論的聯系　角谷靜夫、卡茨、杜佈等人首先發現瞭佈朗運動與古典位勢論有密切的聯系；亨特則發現通過一大類非常返馬爾可夫過程可以深入研究位勢論；後來，F.L.斯皮策用隨機遊動，J.G.凱梅尼和J.L.斯內爾用馬爾可夫鏈首先研究瞭常返的位勢理論。

　　位勢論與概率論的密切聯系，最明顯的是，決定一個馬爾可夫過程的轉移函數可以用來定義位勢論中的格林函數。位勢論中的許多概念和原理都有明確的概率意義，特別體現在上鞅理論中，比如上調和函數相應於上鞅。位勢論中的法圖型邊界極限理論相應於上鞅收斂理論；單調上調和函數列的極限性質與單調上鞅的極限過程性質頗為相似；某些上調和函數、上鞅稱為位勢，它們在各自的理論中都有與之關聯的測度，都遵從隻涉及這些測度支柱的控制原理，以及在概率論與位勢論中，都存在一個性質相同的簡化測度，它導出與位勢相關聯的測度的掃除等等。

　　以佈朗運動為例，設x(t)，t≥0為Rⁿ上的標準佈朗運動，{p_x}，x∈Rⁿ為相應的概率測度族，p_x以

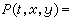
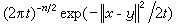為密度，而 p( t， x， y)構成強馬爾可夫轉移半群。令 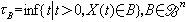（ B ⁿ為波萊爾代數），稱τ _B為 x( t)首中 B的時間，稱 T _B=τ 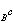為首退出 B的時間。若對任意 x∈ R ⁿ都有 p _x(τ _B＜∞)=0，則說 B是極集；若 p _x(τ _B=0)=1，則說 x是 B的正則點。對 n≥3，令

，

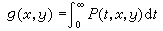
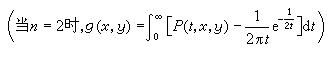則 g μ（ μ是拉東測度）就是牛頓位勢（當 n=2時為對數位勢），極集是牛頓零容集。

　　設區域

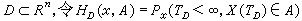， A∈ B ⁿ稱為佈朗運動的退出分佈，則 H _D( x，·)就是 D在 x點的調和測度。又設 φ( x)在д D基本有界，則

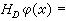
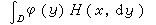就是廣義狄利克雷問題的解。令 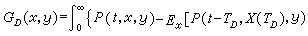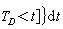； 則 G _D( x， y)就是 D上的格林函數。如果 u是上調和函數，在滿足一些適當的條件後， u( x( t))是上鞅。

　　在馬丁空間也可以構造佈朗運動。此外，利用隨機積分方程的方法可以構造一般C^∞級流形上的擴散過程，因此可以用概率方法研究馬丁空間和C^∞黎曼流形上的位勢論。由於位勢論與概率論存在密切的聯系，使得位勢論有瞭明顯的概率意義而位勢論也為概率論的研究提供瞭一種新的有力的分析工具。

　　

參考書目

　N.S.Landkof，Foundations of Modern Potential Theory，Springer-Verlag，Berlin，1972.

　M.Brelot，On Topologies and Boundaries in Potential Theory，Springer-Verlag，Berlin，1971.

　C.Constantinescu and A.Cornea，Potential Theory on harmonic Space，Springer-Verlag，Berlin，1972.

　C.Berg and G.Forst，Potential Theory on Locally Compact Abelian Groups，Springer-Verlag，Berlin，1975.

　J.L.Doob，Classical Potential Theory and Its Probabilitic Counterpart，Springer-Verlag，New York，1984.

　M.Tsuji，Potential Theory in Modern Function Theory，Maruzen，Tokyo，1959.