一類拓撲空間。重要性在於許多常見的空間屬於這一類;另外同倫論的方法對這類空間能較好地發揮。單純複形(見拓撲學,同調論)是CW複形的特例。粗略地說,CW複形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。同倫論中往往需要在拓撲空間上定義滿足某種條件的連續映射。這對非常一般的拓撲空間來說很難著手。但對於CW複形,則可以從低維到高維,在一個一個胞腔上給出定義,即採用“逐層擴張”的方式得到所需要的連續映射。如果擴張到某一層遇到阻礙,就產生阻礙上閉閉鏈,阻礙上同調類等等(見同倫論),這樣就能利用同調來討論關於連續映射的擴張或同倫等問題。
設X為豪斯多夫空間,{e
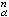 }為
X的一組子空間,α∈
J
n(
J
n為標號集合),
n=0,1,2,…,記
}為
X的一組子空間,α∈
J
n(
J
n為標號集合),
n=0,1,2,…,記
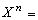

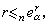
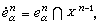
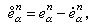 並且設下列條件成立:
並且設下列條件成立:
①
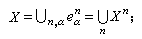
②
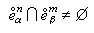 蘊涵
n=
m,α=
β;
蘊涵
n=
m,α=
β;
③ 對任意一對n,α,有連續映射
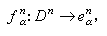 滿足
滿足
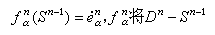 同胚地映為 ė
同胚地映為 ė
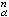 ,其中
D
n為歐氏空間
R
n裡的單位球體,
S
n
-1為
D
n的邊界球面。這時稱集合
,其中
D
n為歐氏空間
R
n裡的單位球體,
S
n
-1為
D
n的邊界球面。這時稱集合
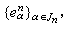 n=0,1,2,…構成空間
X的一個胞腔剖分,
e
n=0,1,2,…構成空間
X的一個胞腔剖分,
e
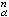 (α∈
J
n)稱為
X的
n維胞腔,
(α∈
J
n)稱為
X的
n維胞腔,
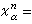
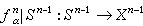 稱為粘貼映射,
X
n稱為
n維骨架。條件①、②、③蘊涵
稱為粘貼映射,
X
n稱為
n維骨架。條件①、②、③蘊涵
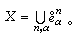 具備瞭一個胞腔剖分的豪斯多夫空間叫作胞腔復形。
具備瞭一個胞腔剖分的豪斯多夫空間叫作胞腔復形。
若
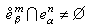 ,則稱
e
,則稱
e
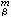 為
e
為
e
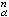 的一個直接面。
e
的一個直接面。
e
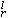 稱為
e
稱為
e
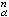 的一個面,如果二者之間可以插入一列有限多個胞腔使得前一個為後一個的直接面。
的一個面,如果二者之間可以插入一列有限多個胞腔使得前一個為後一個的直接面。
胞腔復形X稱為CW復形,假如下列條件滿足:
C:閉包有限──每個胞腔隻有有限多個面;
W:弱拓撲──子集S⊂X為閉集當而且僅當對一切n,α,S∩e
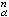 為
e
為
e
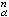 中的閉集。
中的閉集。
例如,在球面Sn中,任取一點p∈Sn,令e0=p,en=Sn,則Sn剖分成瞭隻含兩個胞腔{e0,en}的胞腔復形。
又如,在實射影空間RPn中,有一個由n+1個胞腔e0,e1,…,en構成的胞腔剖分,亦即每個維數恰好有一個胞腔。
上面已經提到,CW復形X可看作是逐層粘貼胞腔而得到的:X0為若幹個點;設Xn-1已粘好,用粘貼映射x
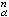 將
D
n粘貼到
X
n
-1上得到各個
e
將
D
n粘貼到
X
n
-1上得到各個
e
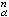 ,從而造出
X
n,……。
,從而造出
X
n,……。
同一個空間可以有不同的胞腔剖分。一般胞腔剖分比單純剖分所含有的胞腔總數可以少得多,這是胞腔剖分的一大優點。