仿射平面（或空間）到自身的一類變換，最重要的性質是保持點的共線性（或共面性）以及保持直線的平行性。作為最常見的例子，首先引進兩平面間的平行投影，設已知兩平面π與π′，d是與兩平面都不平行的向量，過平面π上各點A、B、C、…分別作與d平行的直線交π′於A′、B′、C′、…，於是π與π′各點間存在著一一對應的關系，這項對應關系叫做π到π′的平行投影。A與A′，B與B′，C與C′…為平行投影下的對應點，顯見平行投影與d有關。兩平面間的平行投影具有以下重要性質：點變點；直線變直線；點與直線的結合關系不變。共線三點的簡比不變，即
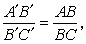其中
A′、
B′、C′分別是共線三點
A、
B、C的對應點，平面
π上的兩條平行線，對應著平面
π′上的兩條直線，也是平行的（圖1
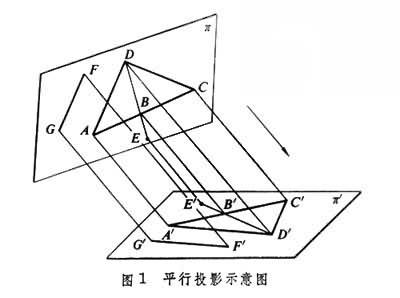）。當把
π經過一系列平行投影，最後仍變到
π本身的一一變換，就是一個仿影變換。在此情況下，上述性質也是保留的。將平行投影的概念加以推廣，即得到下面的重要概念。
兩平面間的一一對應，如滿足共線三點的對應點仍是共線三點；則此一一對應，叫仿射對應。如果兩平面重合，就叫平面到它本身的仿射變換。因為仿射變換之積，仍是仿射變換；任一個仿射變換的逆，仍是仿射變換，故平面內所有仿射變換的集合成群(見變換群)，叫做仿射變換群。它是射影變換群的子群。類似地可定義空間的仿射變換及仿射變換群。
仿射性質與仿射不變量 按照依變換群將幾何學分類的觀點，圖形在仿射變換群下的不變性質和不變的量叫做仿射性質和仿射不變量。研究圖形仿射性質的幾何分支就稱為仿射幾何學。例如同素性（點變成點，直線變成直線）、結合性（點在線上或直線通過點）都是基本的仿射不變性，簡比則是基本的仿射不變量。而且還可推出，二直線的平行性、平行線段的比、封閉圖形面積的比等，都是在仿射變換下不變的。又如關於二次曲線的中心、直徑及共軛徑等，都是平面仿射幾何的研究對象，因為它們都是仿射性質。
仿射坐標系 見坐標系。
仿射變換的代數表示 設給定平面上一個仿射坐標系{O；e1，e2}，仿射變換將點P變為點P′，並將坐標系{O；e1，e2}變為坐標系{O′；e1′，e2′}(圖2
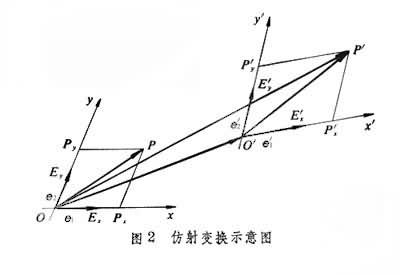)。若令
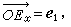
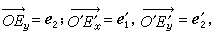則
e
1，
e
2；
e
1
′，
e
2
′分別為新舊兩坐標軸上的坐標向量。設
P，
P′，
e
1
′，
e
2
′，
O′在{
O；
e
1，
e
2}下的坐標，分別是
P(
x，
y)，
P′(
x′，
y′)，
e
1
′(
α
11，
α
21)，
e
2
′(
α
12，
α
22)，
O′(
α
13，
α
23)，如果要求出
P與
P′坐標間的關系。由於仿射變換保持平行性，故
O′
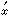P
P′
P
仍為平行四邊形，又由於仿射變換保持簡比不變，所以
P′在{
O′；
e
1
′，
e
2
′}下的坐標仍為(
x，
y)。根據向量的加法及向量的坐標表達，則有：
又
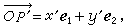比較以上二式，得
(1)
由於
e
1
′，
e
2
′不平行，故又有
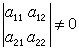(2)
滿足(2)的(1)式，就是仿射變換的代數表示式。利用仿射變換的代數表示，對問題的解決將有很大的方便，同時也便於將它推廣到高維空間。