一種特殊的三角級數。形如

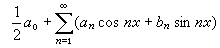　　　(1)

的級數，其中 α n( n=0，1，2，…)和 b n( n=1，2，…)是與 x無關的實數，稱為 三角級數。特別，當(1)中的系數 α n， b n可通過某個函數 f( x)用下列公式表示時，級數(1)稱為 f的傅裡葉級數：

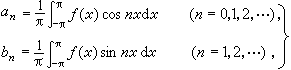　　　(2)

式中 f是周期2 π的可積函數，即 f∈ l 1(- π， π)。此時，由公式(2)得到的系數 α n， b n稱為 f的傅裡葉系數。 f的傅裡葉級數記為

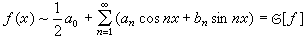。　　　(3)

當然， f的傅裡葉級數並不一定收斂；即使收斂，也不一定收斂於 f( x)。假如已知三角級數一致收斂於 f( x)，即 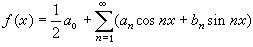，那麼雙方都乘以 cos nx或sin nx後，在(－ π， π)上可以逐項積分，由三角函數系的正交性，即得公式(2)。所以，如果三角級數(1)一致收斂於 f( x)，級數(1)必為 f的傅裡葉級數。

　　問題往往是，給定函數f，需要把它表示成三角級數(1)。J.-B.-J.傅裡葉的建議是，利用公式(2)，求出f的傅裡葉系數αn，bn，就得到傅裡葉級數(3)。可以證明，隻要f滿足一定的條件，那麼f的傅裡葉級數σ[f]收斂於f。

　　傅裡葉級數的收斂判別法　常用的判別法有：

　　① 迪尼判別法　對固定的點x，如有數s，使得函數φx(u)/u=(f(x+u)+f(x-u)-2s)/u在[-π，π]上勒貝格可積，則σ[f]在點x收斂於s。由此可知，當f在點x連續，並滿足李普希茨條件，即

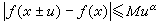(0＜ u≤ h)，那麼σ[ f]在 x收斂於 f( x)，其中 M， h， α均為正數，且 α≤1。另外，當 f( x)具有連續的導函數 f′( x)時，σ[ f]一致收斂於 f( x)。

　　② 狄利克雷－若爾當判別法　假設函數f在含有點x的某區間，例如［x-h，x+h］上分段單調，則f的傅裡葉級數在點x收斂於(f(x+0)+f(x-0))/2。

　　上面提到的收斂判別法，對函數所提的要求，都是充分條件，並非必要的。關於收斂性判別法，還有幾種。值得註意的是，至今還沒有收斂的充分且必要的條件。

　　傅裡葉級數的復數形式　三角級數(1)還可用指數函數來表示。事實上，

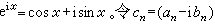/2， （ C n表示с n的共軛復數），那麼級數(1)可寫成復數形式

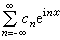，　　　(4)

這裡，(4)的部分和 S n理解為 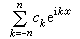。假如(1)是 f的傅裡葉級數，那麼它的復數形式也是(4)，但系數

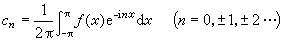。　　　(5)

上式表達的с n稱為 f的復傅裡葉系數，又稱 f的傅裡葉系數的復形式。

　　傅裡葉系數的重要性質　列舉下面兩條：

　　① 若f(x∈l(-π，π)，則f的傅裡葉系數αn，bn（或сn），當n→∞時趨於0，稱為黎曼-勒貝格定理。

　　② 若f(x∈l2(-π，π)，則有

。

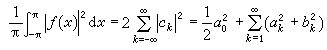這個等式稱為帕舍伐爾等式；反之假如{с k}是一列雙向的數列，滿足條件 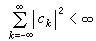，那麼必存在惟一的函數 f( x∈ l 2(- π， π)，它的傅裡葉系數等於｛с k｝( k=0，±1，±2，…)。這個逆命題稱為裡斯－費希爾定理。

　　三角級數與單位圓內解析函數的關系　設z=eix(0≤x＜2π)是復平面單位圓周上的點，於是級數

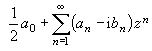　　　(6)

的實部就是三角級數(1)，虛部

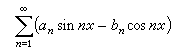　　　(7)

稱為三角級數(1)的共軛級數。假如(6)中的 z表示單位圓內的點，即 z= re ix(0≤ r＜1)，那麼(6)就是復變數 z= r e ix的冪級數，當它收斂時，其和函數是單位圓內的解析函數。所以三角級數(1)可以看做單位圓內解析函數邊界值的實部。

　　多元三角級數與多元傅裡葉級數　設

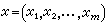為 m維歐氏空間 R m的點，級數

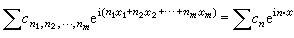　　　(8)

稱為 m元三角級數，其中 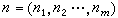，而 n 1， n 2，…， n m為整數。假如 f( x)＝ f( x 1， x 2，…， x m)關於每個變量 x i(1≤ i≤ m)都是周期為2 π的周期函數，且在立方體

Q：-π≤xj≤π　(j=1，2，…，m)　　　(9)

上， f是勒貝格可積的。類似於(5)，如果(8)中系數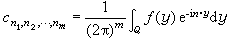

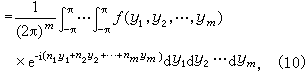那麼稱(8)為 f的傅裡葉級數，並記為

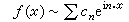多元傅裡葉系數也有類似於一元傅裡葉系數的許多性質，但多元三角級數與多元傅裡葉級數的許多問題，卻遠較一元復雜。在中國，程民德最早系統研究多元三角級數與多元傅裡葉級數。他首先證明多元三角級數球形和的惟一性定理，並揭示瞭多元傅裡葉級數的裡斯-博赫納球形平均的許多特性。

　　傅裡葉級數在數學物理以及工程中都具有重要的應用。

　　

參考書目

　A.Zygmund，Trigonometric Series，Vol.1～2，Cambridge Univ.Press，Cambridge，1959.