研究晶體中的原子在平衡位置附近的振動和這些振動對晶體性質的影響的學科。它是固體物理的基礎之一。
歷史 點陣動力學的研究始於20世紀初。1907年,A.愛因斯坦發表瞭題為“普朗克輻射理論與比熱的理論”的論文,他把N個原子組成的晶體,看作是3N個相互獨立的具有同一頻率的諧振子;並認為這些振子的能量也應按普普朗克的理論量子化,從而說明在溫度趨於絕對零度時,晶體中由原子運動貢獻的比熱趨向於零這一實驗事實。愛因斯坦的工作不僅是點陣動力學的開始,而且在量子理論的發展上也起瞭重要作用。但他所得到的熱容公式在低溫下接近於零的趨向顯得比實驗結果快(見愛因斯坦模型)。P.J.W.德拜在1912年認識到,愛因斯坦熱容公式與實驗不大符合的原因在於沒有考慮到晶體中原子振動頻率並不是完全相同的。德拜把晶體當成連續媒質來求得振子頻率分佈,得到瞭更符合實驗結果的比熱容公式,德拜的理論能比較簡明地概括實驗材料,在推動點陣動力學的發展上,起過較大作用(見德拜模型)。同年,M.玻恩和T.von卡門發表瞭題為“論空間點陣的振動”的論文,提出晶體中的原子振動應以點陣波的形式存在。他們的論文包含瞭現代點陣動力學的大部分基本概念和原則,是點陣動力學的奠基性著作。從20年代到40年代,人們進一步完善瞭點陣動力學的基本理論;點陣振動對晶體的熱力學性質、熱傳導、電導、介電和光學性質、X射線衍射等方面的理論和實驗研究也發展瞭起來。這些都比較完全地總結在玻恩和黃昆的專著《晶體點陣的動力理論》一書中。50年代以來,點陣動力學在實驗研究上有瞭很大的進步,特別是利用中子非彈性散射直接測定點陣振動的色散關系(見點陣動力學的實驗研究方法)。
研究內容 點陣動力學主要研究以下幾個方面。
基本概念 如果不考慮晶體邊界的影響,可以認為討論的是一個無限的晶體點陣。設每個元胞中有 s個原子,元胞L中第k個原子的位置記作
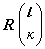 ,它的平衡位置記作
,它的平衡位置記作
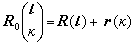 ,
r(
L是元胞
L的位置的點陣矢,
r(
k)是第
k個原子在元胞
L中的相對位置。原子對平衡位置的偏離記作
,
r(
L是元胞
L的位置的點陣矢,
r(
k)是第
k個原子在元胞
L中的相對位置。原子對平衡位置的偏離記作
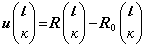 。在絕熱近似下,可以認為晶體原子相互作用的勢能僅是原子的位置的函數,原子的平衡位置是它的極小值。把勢能函數展開為對平衡位置的偏離的級數,顯然,一次項應為零;如果隻考慮到二次項,便得到勢能函數
φ的二次近似展開式
。在絕熱近似下,可以認為晶體原子相互作用的勢能僅是原子的位置的函數,原子的平衡位置是它的極小值。把勢能函數展開為對平衡位置的偏離的級數,顯然,一次項應為零;如果隻考慮到二次項,便得到勢能函數
φ的二次近似展開式
 (1)
(1)
式中
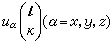 是
是
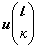 的三個分量。
的三個分量。
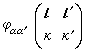 稱為力常數,這個近似稱為簡諧近似。顯然,它應該隻依賴於
L-
L′,而不是分別依賴於
L和
L′。從式(1)可得到點陣中原子的運動方程
稱為力常數,這個近似稱為簡諧近似。顯然,它應該隻依賴於
L-
L′,而不是分別依賴於
L和
L′。從式(1)可得到點陣中原子的運動方程
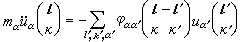 , (2)
, (2)
式中
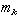 是第
k個原子的質量。這是一個無窮維的周期性的方程。顯然,它有下列波動形式的解
是第
k個原子的質量。這是一個無窮維的周期性的方程。顯然,它有下列波動形式的解
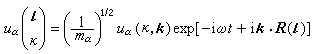 ; (3)
; (3)
式中k是波矢,因此uα(k,k)滿足的方程是
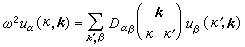 。 (4)
。 (4)
這是一組3s維的方程。其中系數是
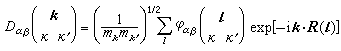 , (5)
, (5)
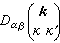 稱動力矩陣。式 (4)有解的條件是系數行列式為零:
稱動力矩陣。式 (4)有解的條件是系數行列式為零:
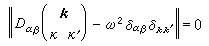 , (6)
, (6)
式中δ是克羅內克符號,即當 α=β時,
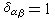 ;反之
;反之
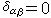 。因此,給定一個波矢
k,從式(6)可得到
3
s個頻率
ω=
ω
j(
k),(
j=1,…,
3
s),把每個頻率代入式(4)得到一支點陣波:
。因此,給定一個波矢
k,從式(6)可得到
3
s個頻率
ω=
ω
j(
k),(
j=1,…,
3
s),把每個頻率代入式(4)得到一支點陣波:
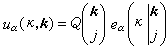 , (7)
, (7)
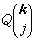 是指這支波矢為
k,頻率為
ω
j的點陣波的振幅。
是指這支波矢為
k,頻率為
ω
j的點陣波的振幅。
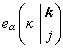 是一個歸一化的
3
s維的矢量
是一個歸一化的
3
s維的矢量
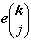 的分量,它表示振動的方向。這樣得到的
3
s支點陣波中,其中有三支是與把晶體看作連續媒質時的三支彈性波相對應,它們的頻率
ω
j(
k)在
k趨於零時應趨於零。這三支稱聲頻支或點陣波的聲頻模。另外的
3
s-3支稱光頻支或點陣波的光頻模。
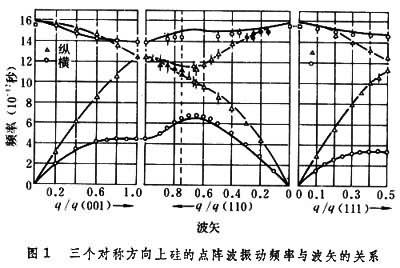
k→0時的光頻支反映瞭元胞中原子的相對振動。圖1是三個對稱方向上矽的點陣波振動頻率與波矢的關系。
的分量,它表示振動的方向。這樣得到的
3
s支點陣波中,其中有三支是與把晶體看作連續媒質時的三支彈性波相對應,它們的頻率
ω
j(
k)在
k趨於零時應趨於零。這三支稱聲頻支或點陣波的聲頻模。另外的
3
s-3支稱光頻支或點陣波的光頻模。
k→0時的光頻支反映瞭元胞中原子的相對振動。圖1是三個對稱方向上矽的點陣波振動頻率與波矢的關系。
兩個波矢相差一個倒易點陣矢量的點陣波是等效的,因此可把點陣波的波矢 k的取值范圍限於波矢空間的特定的多面體,它稱為第一佈裡淵區。k的允許值取決於對解所加的邊界條件。很顯然,對足夠大的晶體來說,選擇不同的邊界條件對從解所得到的晶體的“體”的性質是不會有影響的。H.韋耳(1911)、W.萊德曼(1944)對此給出過嚴格的數學證明。通常,都采用玻恩和T.von卡門的做法,想像把晶體取成為每邊有L個元胞的立方體,要求該立方體相對的面上的解相等。這個邊界條件限制瞭波矢k的取值為
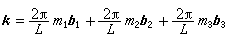 ,
m
1、
m
2和
m
3是整數
b
1、
B
2和
B
3是點陣的倒易點陣的基矢。顯然,在第一佈裡淵區中
k的取值可以有
L
3個,即這個立方體所包含的元胞數。每個
k有
3
s個點陣波,因此共有
3
s
N(
N=
L
3)個點陣波。晶體中任一個原子的運動可以用這
3
s
N個點陣波的疊加來表達。註意到這個立方體中包含有
s
N個原子,有
3
s
N個運動自由度;所以用點陣波來表達可以看作是對這個振動系統的一個坐標變換,從這個觀點,就很容易把點陣動力學的理論發展成為量子理論。
,
m
1、
m
2和
m
3是整數
b
1、
B
2和
B
3是點陣的倒易點陣的基矢。顯然,在第一佈裡淵區中
k的取值可以有
L
3個,即這個立方體所包含的元胞數。每個
k有
3
s個點陣波,因此共有
3
s
N(
N=
L
3)個點陣波。晶體中任一個原子的運動可以用這
3
s
N個點陣波的疊加來表達。註意到這個立方體中包含有
s
N個原子,有
3
s
N個運動自由度;所以用點陣波來表達可以看作是對這個振動系統的一個坐標變換,從這個觀點,就很容易把點陣動力學的理論發展成為量子理論。
在簡諧近似下,這個晶體的哈密頓量是
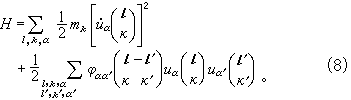
如選擇另一組簡正坐標,作以下的坐標變換:
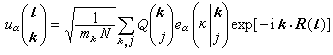 (9)
(9)
代入式(8),考慮到
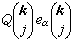 的定義和滿足的條件,就能得到
的定義和滿足的條件,就能得到
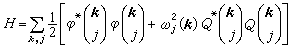 。 (10)
。 (10)
這是 3Ns個相互獨立的諧振子組成的系統的哈密頓量。振子有頻率分佈ωj(k)。因此,通常說點陣波是點陣振動的簡正模。當然,簡正模可有幾種不同的但是是等效的選法。這裡選的是行波式的簡正模,在上述坐標變換的基礎上,如果把簡正坐標
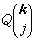 及
及
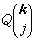 當成量子力學的力學量,不難建立起點陣動力學的量子力學形式。
當成量子力學的力學量,不難建立起點陣動力學的量子力學形式。
點陣振動的頻譜與點陣的熱力學函數 有瞭ωj(k),就可求得在簡諧近似下點陣的熱力學函數。例如內能
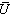 和定容熱容
D
v就是
和定容熱容
D
v就是
 (11)
(11)
式中kB是玻耳茲曼常數。可以引入點陣振動頻譜來進行這些計算。頻譜 g(ω)的定義是在頻率ω附近單位頻率區間中的點陣波模的數目。因此,式(11)可寫為
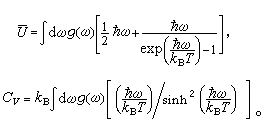
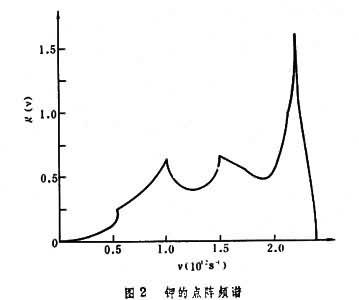
由已知的ωj(k)來求g(ω)是一個數學問題。圖2是從中子非彈性散射實驗測得的鉀的ω(k)計算得到的頻譜g(ω)。圖上看到g(ω)並不是很平滑的函數。其實頻譜上經常會有一些奇異性,這是各類元激發的譜常有的一種現象。
德拜模型相當於假定瞭一種特別簡單的頻譜形式
 (12)
(12)
B由
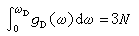 來決定。因此,德拜譜隻有一個參數
ω
D。把
g
D(
ω)代入
D
v的表達式,在
T比較低時,可得到點陣定容熱容的
T
3規律
來決定。因此,德拜譜隻有一個參數
ω
D。把
g
D(
ω)代入
D
v的表達式,在
T比較低時,可得到點陣定容熱容的
T
3規律
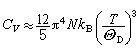 ,
,
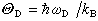 稱德拜溫度。Ⓗ
D作為材料點陣振動頻率的一個粗略估計,有一定參考意義。但如果真正用德拜模型的熱容公式來處理實驗測得的比較精確的熱容數據,就會發現得到的Ⓗ
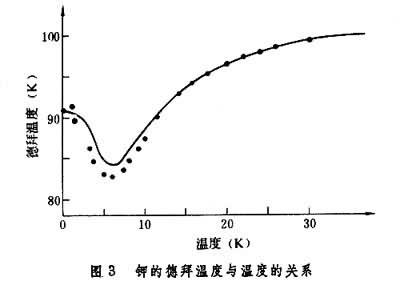
D乃是溫度的函數,考慮到德拜的頻譜與實際頻譜的差異很大,這是很自然的。圖3給出的是這樣處理鉀得到的結果,所以,必須註意德拜模型的適用性。
稱德拜溫度。Ⓗ
D作為材料點陣振動頻率的一個粗略估計,有一定參考意義。但如果真正用德拜模型的熱容公式來處理實驗測得的比較精確的熱容數據,就會發現得到的Ⓗ
D乃是溫度的函數,考慮到德拜的頻譜與實際頻譜的差異很大,這是很自然的。圖3給出的是這樣處理鉀得到的結果,所以,必須註意德拜模型的適用性。
但隻基於簡諧近似來計算晶體的熱力學性質仍是不夠的(見非諧相互作用)。
極性振動與晶體的介電性質和光學性質 離子晶體中,正負離子的相對位移會產生電偶極矩。長波的光頻模相應於元胞中原子的相對移動,可以按它是否產生電偶矩來把它區分為極性振動和非極性振動兩類。極性振動必定伴隨著宏觀的電磁場。因此,必須同時考慮點陣運動的方程和電磁場的方程。黃昆(1951)最先對立方晶體元胞中有兩個離子的情況作瞭系統的處理。這時,應有三個光頻支:一個縱波和兩支橫波,都是極性振動。縱波與橫波有一個顯著不同,縱波會產生束縛電荷,出現宏觀的庫侖場,所以長波的縱光頻支比橫光頻支有較高的頻率。可以證明,在這種情況,波矢趨於零的縱光頻支頻率
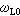 與橫光頻支頻率
與橫光頻支頻率
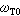 之間有下列關系
之間有下列關系
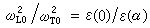 , (13)
, (13)
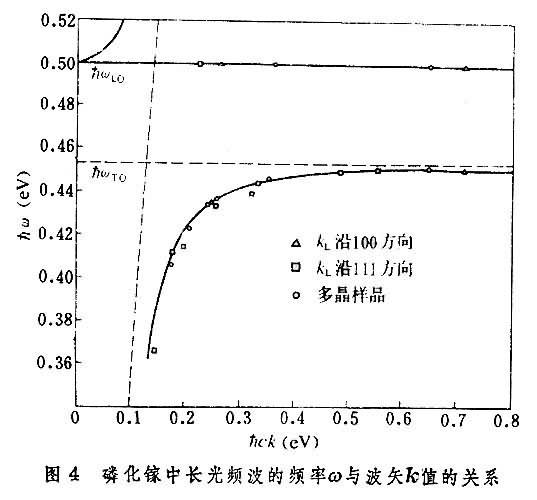
ε(0)是晶體的靜電介電常數。ε(∞)是頻率遠高於點陣振動頻率時的介電常數。這關系稱為 LST關系。橫波則能與外來的電磁波耦合,對點陣的介電性質有貢獻。電磁波和橫向極性振動的耦合產生瞭新的耦合模式,它是電磁波與點陣波的耦合模,稱為極化激元。這是黃昆所首先引入的概念。圖4是實驗上測量得到的磷化鎵中點陣振動的色散關系。虛線是不考慮這個耦合時的色散關系,實線是耦合模式的色散關系。
點陣振動的色散關系與力模型 50年代以來,有瞭準確測定整個佈裡淵區中點陣波的色散關系 ωj(k)的方法(見點陣動力學的實驗研究方法),由此提供瞭定量地檢驗這些理論的可能性。除瞭求解的數學技巧外,這中間最主要的是關於點陣原子間的相互作用的力模型。
最易想到的是所謂“剛性離子”模型,把晶體勢看作是各對原子之間的勢能之和,並認為它隻決定於這個原子之間的距離:
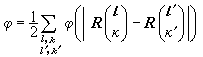 。 (14)
。 (14)
對微小位移偏離作展開,每對原子之間便有兩個力常數──徑向的和切向的。經驗證明,對固態惰性元素和簡單金屬來說,適當選擇力常數,剛性離子模型能給出與某些實驗相當符合的結果。從嚴格的剛性離子模型出發,可導出彈性常數應滿足柯西關系;但對多數金屬(包括堿金屬)來說,柯西關系都符合得相當不好。所以需要對這問題作進一步研究。
對離子晶體和價鍵晶體,經驗證明,殼層模型更合適一些。它把每個原子(離子)看作是由一剛性的“實”和一帶電的“殼”組成,實和殼之間近似地由一各向同性的力常數表征其聯系;同一原子的實和殼之間也可相對移動;不同原子之間的相互作用則包括各自的實和殼相互之間的各種組合。殼層模型是一個唯象的模型。從能帶論和多體理論的觀點也提供瞭它的適用性的一定理論基礎。
相變和點陣振動 F.林德曼(1910)曾提出,固體的熔化發生在點陣振動的平均振幅與原子之間的距離可以比擬的情況下。實驗數據表明這個觀念有一定的合理性,同一類固體的這個比例還常常是差不多的。但一個嚴格的關於熔化與點陣振動之間的關系的理論還沒有建立起來。在結構相變(見固體中的相變)中,點陣振動起著關鍵的作用。
參考書目
M. Born and T.von Karman, Physik Z.,J.-Nr.13,S. 297,1912. M.Born and K.Huang, Dynamical Theory of CrystalLαttices,Oxford Univ.Press, London and New York, 1954.