黎曼流形上的具有特殊性質的各種變換群，其中最重要的是等距變換群（又稱運動群）、射影變換群和共形變換群。它主要研究黎曼流形上的各種變換群的不變性質以及容有各種變換群的黎曼流形的幾何性質和拓撲性質。
設f是黎曼流形(M，g)到自身上的一個微分同胚。在局部坐標系下，設
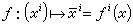，如果成立
，
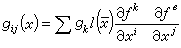即
f保持度量張量
g不變，則稱
f是一個等距變換（又稱運動）。它是歐氏空間的運動在黎曼流形上的推廣。在等距變換下，切向量的長度、交角以及兩點之間的距離均保持不變，測地線變到測地線。N.E.斯廷羅德和S.B.邁爾斯證明瞭：
M上所有的等距變換依變換的乘法構成一個李群。這個群稱為
M的最大等距變換群（又稱完全運動群），相應的子群稱為
M的等距變換群(或運動群)。設
M上一個向量場
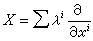所生成的單參數變換群為
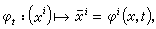即
φ
i滿足方程
，
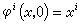，如果對任一
t，
φ
t都是等距變換，就稱
φ
t為單參數等距變換群或稱
X為無窮小運動（又稱基靈向量場）。
X為無窮小運動的充要條件為
X滿足基靈方程
，
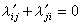這裡“′”表示協變導數，
。
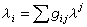n維黎曼流形M的最大等距變換群的參數個數至多是
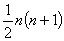個，而達到這個數目時，
M必是常曲率空間。由此可以看出，一個黎曼流形最多能容許含有多少個參數的某種變換群是與流形本身的幾何性質和拓撲性質密切相關的。
G.富比尼首先發現黎曼流形的最大等距變換群的參數個數是有空隙的。後經И.∏.葉戈羅夫、矢野健太郎、若桑英清、王憲鐘等人的研究，確定瞭第一空隙，即
n維黎曼流形不容許參數個數
r介於
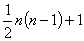與
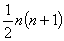之間的最大等距變換群，並且在
n＞243的條件下確定瞭第二空隙。1964年，胡和生給出瞭確定空隙的一般方法並完全確定瞭開首八個空隙和相應空間的局部線素形式。
如果黎曼流形(M，g)到自身上的微分同胚f將測地線變到測地線，就稱f是射影變換。M上所有的射影變換依變換乘法構成的群稱為最大射影變換群，相應的子群稱為射影變換群。在局部坐標下，f是射影變換的充要條件為：存在函數φ，使得成立
，
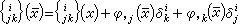這裡
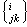是第二類克裡斯托費爾符號，射影變換下最重要的不變張量是下式定義的射影曲率張量
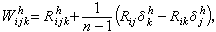式中
，
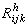R
ij分別是
M的曲率張量和裡奇曲率張量。一個黎曼流形的最大射影變換群的參數個數至多是
n
2+
2
n個，而達到這個數目時，它必定是常曲率空間。向量場
X＝
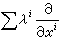生成單參數射影變換群的充要條件為
X滿足方程：
。
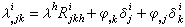如果黎曼流形(M，g)到自身上的微分同胚f保持向量的夾角不變，即在局部坐標系下成立
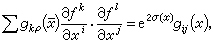式中
σ是某一函數，就稱
f是共形變換。
M上所有的共形變換依變換的乘法構成的群稱為
M的最大共形變換群，相應的子群稱為共形變換群。共形變換下最重要的不變張量是由下式定義的共形曲率張量
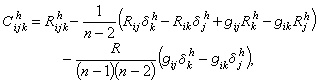這裡
R是數量曲率。一個黎曼流形的最大共形變換群的參數個數至多是
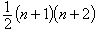個。向量場
X＝
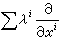生成單參數共形變換群的充要條件為
X滿足方程
。
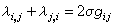參考書目
S.Kobayashi and K.Nomizu，Foundations of Diff-erential Geometry，Vol.1，John Wiley &Sons，New York，1963.
蘇步青編著：《現代微分幾何學概論》，上海科學技術出版社，上海，1961。