概率論中討論隨機變數序列的算術平均值向常數收斂的定律。是概率論與數理統計學的基本定律之一。
以重複投擲一枚硬幣的隨機試驗為例，記n次投幣試驗中出現正面的次數為vn。對於不同的n次試驗，vn可能能不同，但當n越來越大時，出現正面的頻率vn/n將大體上逐漸接近於1/2。又如稱某一物體的重量，假如衡器不存在系統偏差，由於衡器的精度等各種因素的影響，對同一物體重復稱量多次，可能得到多個不同的重量數值X1，X2，…，Xn。但若取它們的算術平均值
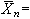
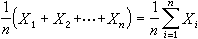，則隨
n的增大，一般來說
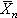也將逐漸接近於物體的真實重量。
歷史上，雅各佈第一·伯努利(1652～1705)在《推測術》(1713年出版)中首先從數學上論述瞭這一現象。他證明瞭：若vn是n次獨立重復試驗中事件A出現的次數，p是事件A的概率，則對任一ε>0，有
，即
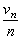依概率收斂於
p。這一結論表明，對任意小的正數ε，隻要
n充分大，頻率
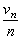與概率
p發生大於ε的偏離的可能性就很小，即大多數試驗隻使
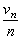與
p發生較小的偏離。這是歷史上第一個嚴格說明頻率穩定性的定律，稱為伯努利大數律。大數律這個名稱是
S.-D.泊松於1837年給出的。大數律表明，對同一隨機變量
X的
n次獨立觀察值
X
1，
X
2，…，
X
n的平均，將隨
n的增大而收斂於它的
數學期望
E
X。在數理統計中，就依據這一點而取多次重復觀測的算術平均作為E
X的較精確的估計。特別可以利用頻率的穩定性來對事件的概率和隨機變量的分佈進行估計，還可以利用樣本矩向總體矩的收斂，取樣本矩作為總體矩的近似而獲得參數估計的矩方法（見
點估計）。
由於隨機變量序列
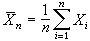向常數的收斂可以有多種不同的方式，按其收斂為依概率收斂、以概率1收斂或均方收斂（見
概率論中的收斂），分別有弱大數律、強大數律或均方大數律。弱大數律又通稱為大數律。根據隨機變量序列各種收斂之間的關系，由強大數律或均方大數律可以推出弱大數律。
大數律中最重要的一類是討論獨立試驗序列的，常見的除瞭伯努利大數律外，還有下列著名的大數律：
辛欽大數律(1929) 若{Xn}為獨立同分佈隨機變量序列，EXn=μ存在有限，則對任何ε>0，有
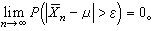
波萊爾強大數律(1909) 設vn是n次獨立重復試驗中某事件A出現的次數，P(A)=p，則以概率1成立
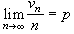。(F.-É.-J.-) É.波萊爾最初隻證明瞭
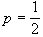的情形，以後才證明瞭對一般的
p也有同樣的結果。
柯爾莫哥洛夫強大數律 若{Xn}為獨立同分佈隨機變量序列，EXn存在，則以概率1成立
。
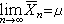大數律中涉及到的隨機變量序列{Xn}也可以不是相互獨立的。特別對於平穩序列，x可看為序列按時間的平均，而 EXn=μ是同一時刻不同樣本的統計平均。這時，
→
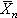μ表明{
X
n}隨時間的增長遍歷瞭它的各種可能狀態，因而使“時間平均”向“統計平均”收斂。這又稱為平穩序列的遍歷性，它也是一種大數律。在
平穩過程理論中，
Α.Я.辛欽和
G.D.伯克霍夫分別建立瞭
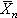向
μ均方收斂和以概率1收斂的遍歷定理。
不僅有算術平均向常數收斂的大數律，更一般地，對隨機變量序列{Xn}，記
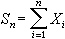，若存在常數序列{
α
n}及趨於無窮的{
b
n}，當
n→
時使
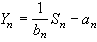依概率或以概率1收斂於零，則分別稱{
Y
n}是依概率穩定或以概率1穩定的。這是大數律的一種推廣形式。由於
Y
n依概率收斂於零與
Y
n的分佈向集中於零的退化分佈弱收斂是等價的，因此弱大數律就是討論
Y
n的分佈向退化分佈弱收斂的極限定理（見
中心極限定理），可作為普遍極限定理的特例來處理。
切比雪夫不等式 若隨機變量的數學期望、方差分別為EX及varX，則對任何α＞0，成立
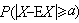
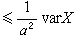。這一不等式是證明弱大數律的重要工具。它在I.－J.比安內梅1853年的論文中已有類似的表述，但直到1867年才由
∏.Л.切比雪夫明確敘述和論證。它對隨機變量的分佈並無特殊要求，僅利用
X的方差來對
X的取值與
E
X發生較大偏離的概率作出估計，因而有較廣泛的適用性。它還有種種推廣形式。若
X為一隨機變量，
f（
x）為一非負非降函數，則
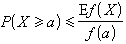，其中
E
f（
X）表示
f（
X）的數學期望。特別當
f(
x)＝
x
λ，
x≥0，
λ＞0，則有
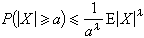。後者又稱為馬爾可夫不等式。
柯爾莫哥洛夫不等式 設｛Xk，1≤k≤n｝是相互獨立的隨機變量，它們的數學期望、方差分別為 EXk＝0，
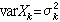，又
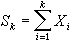，則對任何
α＞0，成立下列不等式：
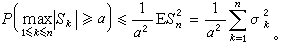若
X
k還是有界的，即|
X
k|≤c以概率1成立，則還有
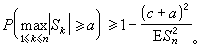這兩個不等式是由
Α.Η.柯爾莫哥洛夫在1928年建立的，它是證明強大數律的重要工具。此外，利用前者可以推出，對獨立的隨機變量序列{
X
n}，若其方差級數
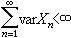，則隨機變量級數
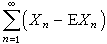以概率1收斂；利用後者可以推出，若有界獨立隨機變量序列的級數
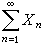以概率1收斂，則其方差級數
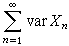和均值級數
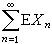都是收斂的。
這一不等式也有各種不同形式的推廣。例如下鞅的極值不等式：設{Yn}為一離散時間下鞅（見鞅），α＞0，則有
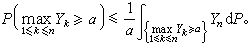此外，若{
X
k，1≤
k≤
n}為相互獨立的隨機變量，
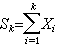；在不要求
X
k存在數學期望與方差的情形，仍成立如下的萊維不等式：
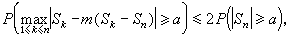式中
m(
S
k-
S
n)表示隨機變量
S
k-
S
n的中位數（見
概率分佈）。這些不等式在證明隨機變量序列以概率1收斂時，都有重要的應用。
波萊爾-坎泰利引理和0-1律 設{An，n≥1}為一事件序列，則由
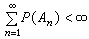可以推出{
A
n}中有無窮個同時發生的概率為0。這一結論稱為波萊爾－坎泰利引理。若進一步設{
A
n}為相互獨立的事件序列，則更有下列的波萊爾0－1律或0－1準則：按照級數
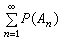收斂或發散，{
A
n}中有無窮個同時發生的概率分別為0或1。這是證明各種以概率1成立的性質的有力工具。
又若用σ(Xk，k≥n)表示由隨機變量序列{Xk，k≥n}生成的事件σ-域，
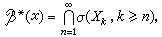那麼，柯爾莫哥洛夫0-1律斷言：對於獨立隨機變量序列{
X
n，
n≥1}，
β
*(
X)中任一事件的概率必為0或1。利用它可以斷定，事件
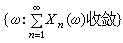及
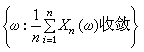的概率為0或1；還可以推出
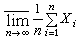以概率1等於某個常值。
重對數律 設｛Xn｝是獨立同分佈的隨機變量序列，
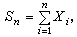且
P(
X
n=1)=
p，
P(X
n=0)=1-
p。強大數律斷言，
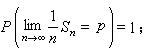即對任何ε>0，不等式
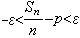除有限個
n外成立的概率為1。辛欽於1924年進一步證明瞭如下的重對數律：
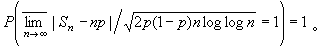由此可以推出，對任何ε >0，不等式
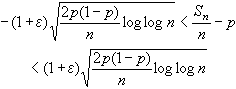除有限個
n外成立的概率為1。這個結果用重對數函數loglog
n描述瞭算術平均值向數學期望收斂的速度，它比通常的強大數律要精確。
對較一般的情形，柯爾莫哥洛夫於1929年證明瞭：若｛Xn｝為獨立隨機變量序列，其數學期望、方差分別為EXn=0，
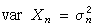，又記
且對某一趨於0的常數列{
X
n}，以概率1成立
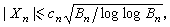則有
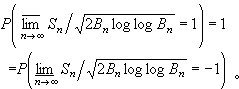P.哈特曼和A.溫特納於1941年更證明瞭，對獨立同分佈的隨機變量序列，上式成立的充分必要條件是
X
n的方差有限。
此後，對更一般的獨立隨機變量序列、鞅差序列(即其部分和為離散時間鞅)、弱相依序列等，都在一定條件下得到瞭類似的結果。
重對數律的證明采用瞭較高深的分析技巧，因而它是概率論極限理論中比較深入和精密的定理。
參考書目
Y.S.Chow and H.Teicher，Probability Theory，Springer-Verlag，New York，1978.