不定方程

　　數論的一個分支，它有悠久的歷史與豐富的內容。所謂不定方程是指解的範圍為整數、正整數、有理數或代數整數等的方程或方程組，一般來說，其未知數的個數多於方程的個數。古希臘數學傢丟番圖於3世紀初就研究過若幹這類方程，所以不定方程又稱丟番圖方程。1969年，L.J.莫德爾的專著《丟番圖方程》，較系統地總結瞭這方面的研究成果。近十多年來，這個領域更有重要進展。雖然如此，從整個地說，對於高於二次的多元不定方程，人們知道得不多。另一方面，不定方程與數學的其他分支如代數數論論、代數幾何、組合數學等有著緊密的聯系，在有限群論和最優設計中也常常提出不定方程的問題，這就使得不定方程這一古老的分支仍然並將繼續吸引著許多數學傢的註意，成為數論中重要的研究課題之一。

　　一次不定方程　最簡單的一次不定方程是二元一次不定方程

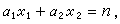(1)

式中α ₁，α ₂， n是給定的整數，α ₁α ₂≠0。

　　在17世紀，已經知道方程(1)有整數解的充分必要條件是(α₁，α₂)能整除n，並當(1)有解時，可用輾轉相除法來求(1)的一組解。

　　設(α₁，α₂)=1，則(1)的全部整數解可表為

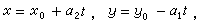(2)

式中 x ₀， y ₀為(1)的一組解， t為任意整數。稱(2)為方程(1)的通解。

　　一般地，s(s≥2)元一次不定方程是指

　　(3)

式中α _i(i=1，…， s)， n都是給定的整數，α ₁α ₂…α _n≠0。

　　與二元的情形類似，方程(3)有整數解的充分必要條件是(α₁，α₂，…，α_s)能整除n。

　　方程(2)的通解含一個參數，方程(3)的通解含s-1個參數。例如，在s=3時，設(α，b，с)=1，(α，b)=d，α=dα′，b=db′，不定方程

(4)

的通解可表為

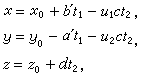式中 x ₀， y ₀， z ₀是(4)的一組解， u ₁、 u ₂滿足 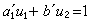， t ₁、 t ₂為任意整數。

　　設α₁＞0，α₂＞0，(α₁，α₂)=1，考慮方程(1)的非負整數解。19世紀，J.J.西爾維斯特曾經證明瞭：在n＞α₁α₂-α₁-α₂時，(1)有非負整數解，但在

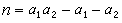時，(1)沒有非負整數解。

　　設α_i＞0(i=1，2，…，s)，（α₁，α₂，…，α_s）=1，考慮式(3)非負整數解x_i≥0(i=1，2，…，s)。容易證明，存在僅與α₁，α₂，…，α_s有關的數

，當 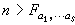時，(3)有非負整數解。求出 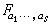的最佳值 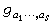，就是著名的弗羅貝尼烏斯問題。當 s=2時，已知 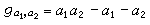，對於 s≥3時，近幾十年來，國內外均有不少工作，特別對 s=3的情形，已找到多種計算 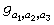的方法。

　　5世紀末，中國數學傢張丘建在他編寫的《張丘建算經》裡提出的“百雞問題”，就是求方程組

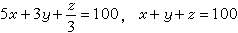的正整數解問題，它是一個一次不定方程組。一次不定方程組可用消元法化為一次不定方程求解。一般的整系數線性方程組可寫為

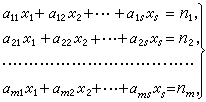　 　 　(5)

式中 m≤ s，設(5)的系數矩陣及其增廣矩陣分別為 A和 B：

。

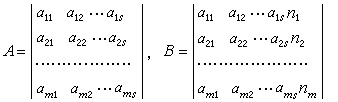(5)有整數解 x _j（ j)=1，2，…， s）的充分必要條件是 D _i= D _i ^′(i=1，2，…， m)，其中 D _i， D _i ^′分別表矩陣 A和 B中諸i行i列子式的最大公因數。當 s= m，│ A│>0時，(5)有整數解的充分必要條件是，對於│ A│的任一個因數 M，同餘式組

有解。對於 n _i=0(i=1，2，…， m)，即齊次的情形，當1≤ m＜ s時，用 抽屜原理可證，此時(5)有不全為零的整數解 x _j，( j=1，2，…， s) 且滿足 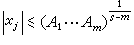( j=1，2，…， s)，這裡 ( j=1，2，…， m)。

　　商高數　滿足不定方程

(6)

的正整數，叫做商高數（勾股數），也叫畢達哥拉斯數。

　　中國古代數學書《周髀算經》中曾經提到“勾廣三、股修四、徑隅五”這個三邊都是正整數的直角三角形，因此，已經知道方程(6)的一組正整數解x=3，y=4，z=5。古希臘數學傢畢達哥拉斯也給出瞭方程(6)的一些正整數解。至少在16世紀以前，已經給出瞭方程(6)的全部正整數解。若(x，y)=d，由(6)有d│z，故可設(x，y)=1，此外，顯然x和y一奇一偶。可證不定方程(6)滿足(x，y)＝1，2|x的全部正整數解可表為x=2αb，y=α²-b²，z=α²+b²，式中α、b為任意整數滿足α>b＞0，(α，b)=1，2磍α+b。

　　在17世紀，上述結果曾給P.de費馬很大影響，導致他提出瞭在數論發展史上非常重要的三個定理。

　　① 每一個形如4k+1的素數p可惟一地表成兩個正整數的平方和，即p=x²+y²，0＜x＜y。

　　② 每一個正整數能夠表成四個整數的平方和。

　　③ 不定方程

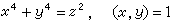　　　　(7)

沒有 x y≠0的整數解。

　　對於第一個定理，費馬說他能夠用無限遞降法證明，但未發表。第一個完全的證明是L.歐拉在1749年給出的，他在1773年和1783年又給出瞭更好的證明。特別是近代，有人把x，y具體表示瞭出來：

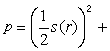
，其中 r， n滿足勒讓德符號

。

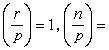
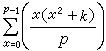　　關於第二個定理，費馬的證明仍未被發現。1772年，J.-L.拉格朗日給出瞭第一個證明，一年後，歐拉給瞭一個更簡單的證明。由於形如8k+7的數不能表成三個整數的平方和，因此，這是一個很完美的定理。而且，這個定理也是非常有用的，例如在組合數學裡的阿達馬矩陣的構造中就要用到。

　　費馬給出瞭第三個定理的證明。他證明這個定理所創造的無窮遞降法至今還很有用。如果(7)有一組整數解x₀，y₀，z₀，x₀y₀≠0，可設z₀＞0，利用方程(6)的整數解公式，可以得出(7)的一組新解x₁，y₁，z₁滿足x₁y₁≠0，z₀＞z₁＞1，這個方法可以繼續下去，從而得到一個無窮的、嚴格遞降的正整數序列z₀＞z₁＞z₂＞…，因為z₀是一個確定的正整數，這當然是不可能的。

　　有一個關於商高數的猜想：設α、b、с是商高數，x、y、z是正整數，且滿足

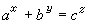，那麼 x= y= z=2。對這個猜想，有過許多工作，但仍未徹底解決。

　　佩爾方程　二次不定方程中，最簡單的也是最重要的方程是佩爾方程。佩爾方程是指不定方程

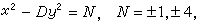(8)

式中整數 D＞0不是平方數。

　　人們最先考慮的是N=1的情形，即不定方程

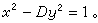(9)

J.佩爾是17世紀的英國人，對方程(9)他並沒有做什麼工作，由於L.歐拉弄錯瞭才冠以他的名字。1766年前後，J.-L.拉格朗日首先證明(9)有 y≠0的整數解。

　　設x₀＞0，y₀＞0是方程（9）的所有x＞0，y＞0的解中使

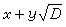最小的那組解，稱 x ₀， y ₀為(9)的最小解，則(9)的全部整數解 x、 y，由 表出，其中 n是任意整數。

　　隻需要求(9)的最小解，它的全體解x、y也就表示出來瞭。最小解也可以定義為方程(9)的整數解x＞0，y＞0中使x最小或使y最小的解。因此，尋找(9)的最小解可以用驗算的方法，令y=1，2，3，4，…，直到1+Dy²是一個完全平方時即可求出。然而，這種方法有時計算十分冗長。例如，x²-94y²=1的最小解是x₀=2143295，y₀=221064。也可把

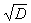展成連分數，那麼 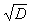的漸近分數 p _n/ q _n中，一定有 k使 x ₀= p _k， y ₀= q _k。如果ζ、η都是正整數，滿足(9)，且有 ，則ζ、η是(9)的最小解。

　　對於不定方程(8)，很明顯，在N=-1時，如果D含有4k+3形狀的素因數，就無整數解。但是如果它有一組整數解，就有無窮多組解。可類似（9）那樣定義它的最小解。如果它有最小解x＝α，y＝b，那麼它的全部解由

給出，其中 n是任意整數，且 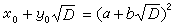， x ₀、 y ₀為(9)的最小解。

　　(8)在N=±4時，有類似的結果。

　　求出佩爾方程最小解的上界，是一個重要問題。設

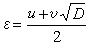， D≡0或1(mod4)是（8）在 N=4時的最小解，1918年，F.舒爾證明瞭 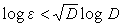。1942年，華羅庚證明瞭 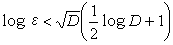。1964年，王元證明瞭對任意 δ>0，皆有常數 C＝ C(δ)，當 D＞ C（δ）時有 。

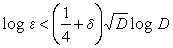　　佩爾方程有許多應用。一般的二元二次方程如果有解，都可歸結為佩爾方程的求解問題，甚至某些二元三次或四次的不定方程也用到它。佩爾方程一個直接的應用是可以證明：在實二次域

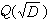中有一個單位數η存在，使得 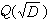中的任一單位數皆可表為±ηη， ⁿ為整數，η叫 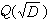的基本單位數。

　　二元二次不定方程　一般的二元二次不定方程可寫為

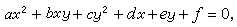　　　(10)

式中α， b，с， d， e，f都是整數。

　　設D=b²-4αс>0，D不是一個平方數，

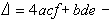
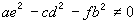， C.F.高斯用佩爾方程證明瞭在上述條件下，若(10)有一組整數解，則有無窮多組整數解。不定方程(10)可用變換的方法歸結為不定方程

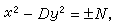　　　(11)

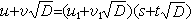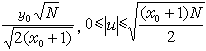不妨設其中整數 D＞0不是平方數， N是一個正整數。1944年，T.內格爾用初等方法，完全決定瞭方程（11）的解。設（ u， v）和（ u ₁， v ₁） 是方程（11）的兩組解，若 ，這裡 s、 t是方程(9)的一組解，則稱( u， v)和( u ₁， v ₁)屬於同一結合類。設 x ₀、 y ₀是與(11)具有相同 D的(9)的最小解，則不定方程 x ²- D y ²= N的解的每一個結合類中，有一個解（ u， v）滿足

；不定方程 x ²- D y ²=- N的解的每一個結合類中，有一個解( u， v)滿足

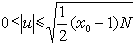，這就證明瞭類數有限，且每一類中的全部解均可表為

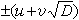
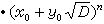， n是任意整數。

　　不定方程αx²+by²=сz²　1785年，A.-M.勒讓德證明瞭：若不定方程

(12)

的系數滿足 α>0， b＞0，с>0，且兩兩互素，都無平方因子，則(12)有一組不全為零且( x， y， z)＝1的解 x， y， z的充分必要條件是 bс，αс，-α b分別是α， b，с的二次剩餘。1950年，L.霍爾澤運用 代數數論證明瞭（12）的非零解滿足 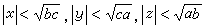。1969年，莫德爾給出瞭霍爾策結果的一個簡單的初等證明。不定方程(12)在組合數學的差集理論中有用。

　　莫德爾方程　設k為整數，不定方程

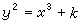(13)

叫做莫德爾方程。

　　三個世紀以來，對不定方程(13)的研究從未停止過，眾多的數學傢運用各種方法研究方程(13)的整數解或有理數解。這些工作豐富和發展瞭數論的內容。17世紀，P.de費馬宣佈他發現一個美妙而精巧的方法，證明瞭方程y²=x³-2僅有整數解x=3。和他的許多定理一樣，他的證明始終沒有被發現。直到1875年，T.佩平給出瞭一個完全的證明：因為x扝0(mod2)和

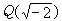中代數整數的惟一分解定理成立，故 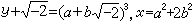，這裡α、 b是整數，因此 b(3α ²- 2 b ²)=1推出 b=1，α=±1， x=3。用同樣的方法可證明方程 y ²= x ³-1僅有整數解 x=1。1912年，莫德爾由於給出方程(13)的一系列新結果，而獲得英國劍橋大學頒發的史密斯獎。1918年，他還證明瞭方程(13)僅有有限組整數解。由於對方程(13)有理數解的研究，引導莫德爾對更一般的曲線上的有理點的研究。1922年，莫德爾猜想：在虧格大於1的代數曲線上僅有有限個有理點。1983年，德國數學傢G.法爾廷斯證明瞭莫德爾猜想，這無疑是20世紀數論中最傑出的工作之一，榮獲1986年 國際數學傢大會的 費爾茲獎。對於有的 k值，方程(13)有時很難解。1930年，T.內格爾證明瞭方程(13)在 k=17時，有8組解：( x， y)=(-2，3)，(-1，4)，(2，5)，(4，9)，(8，23)，(43，282)，(52，375)，(5234，378661)。1963年，W.永格倫完全解決瞭 k=-7， k=-15兩種情形。1968年，A.貝克證明瞭方程(13)的整數解滿足

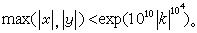
　　圖埃定理　1909年，A.圖埃證明瞭一個重要結果：設n≥3，

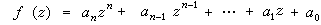是有理數域上一個不可約的整系數多項式，則不定方程

，(14)

僅有有限多組整數解 x， y，式中с是給定的非零整數。

　　這個定理的證明依賴於下列的結果：設θ是一個次數n≥3的整系數不可約多項式的根，則隻有有限組整數x，y＞0適合

。這個不等式， C.L.西格爾在1921年作瞭改進。1958年，K.F.羅特給出瞭最佳結果。如何定出方程(14)解的個數，特別是如何有效地把解計算出來，一直是數學傢們研究的主要問題。1921年，Б.Η.德洛涅證明瞭不定方程

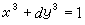(15)

最多隻有一組 x≠0， y≠0的整數解。如果 x ₁、 y ₁是一組解，那麼 是三次域 Q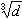（ ）的基本單位數或是基本單位數的平方。1938年，永格倫證明瞭如果某些二次域或四次域的基本單位數能夠決定，那麼，不定方程 A x ⁴- B y ⁴= C的全部整數解也能定出，這裡 A、 B是正整數， C=1，2，4，8或16。

　　運用丟番圖逼近論的方法，1968年，A.貝克給出瞭方程(14)解的一個可計算的上界。他還定出瞭另外許多類不定方程解的上界。貝克的出色工作，曾得到1970年的費爾茲獎。

　　四次方程αy²=bx⁴+с　對於不定方程

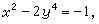(16)

1942年永格倫證明瞭，方程(16)僅有正整數解（ x， y）=(1，1)或(239，13)，但證明很繁，同年他還分別證明瞭不定方程

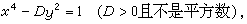(17)

最多有兩組正整數解。以及不定方程

(18)

最多有兩組正整數解，且當解存在時，可有效算出。

　　對於方程（17）、（18）和方程x³+b³=Dy²(b=±1，±2)，永格倫、J.H.E.科恩、柯召和孫琦等，還曾用初等的方法解決瞭其中某些情形。

　　費馬大定理　用不定方程來表示的費馬大定理是：設n＞2，不定方程

(19)

沒有 x y z≠0的整數解。

　　1637年，費馬聲稱他已經證明瞭上述定理，然而他的證明始終未被發現。300多年過去瞭，這個定理至今未能證明，也無法否定。於是後人有把它稱為費馬最後定理、費馬猜想或費馬大問題等。一般傾向性的看法是，費馬那個未曾寫出來的證明是錯的。歷史上，曾有許多優秀的數學傢為瞭證明這個定理，付出瞭巨大的精力。為瞭證明費馬大定理，隻需證明方程

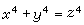，( x， y)=1和方程 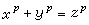，( x， y)=( x， z)=( y， z)=1（ p是一個奇素數）均無 x y z≠0的整數解。費馬本人證明瞭 p=3的情形，但是，這個證明不完全。1823年， A.-M.勒讓德證明瞭 p=5的情形，1839年， G.拉梅證明瞭 p=7的情形，可見進展相當緩慢。以後，數學傢們把費馬大定理中 p磍 x y z叫做費馬大定理第一情形，把 p| x y z叫做費馬大定理第二情形。用初等方法可以證明當 2 p+1， 4 p+1， 8 p+1， 10 p+1， 14 p+1， 16 p+1之一為素數時，費馬大定理第一情形成立，由此可推出 p＜100時，第一情形成立。1847年， E.E.庫默爾對於費馬大定理作出瞭突破性的工作。設 ， h是分圓域 Q(η)的類數，當 p磍 h時， p叫做正規素數。庫默爾證明瞭當 p是正規素數時，費馬大定理成立。通過計算，對於小於100的奇素數中，除開 p=37，59，67以外，都是正規素數。在1847年以後，庫默爾繼續對分圓域進行深入的研究，從而證明瞭 p=37，59，67時，費馬大定理成立。庫默爾為瞭補救一般分圓域中整數環的惟一分解定理不成立而創造的理想數論，豐富和發展瞭代數數論。在近代數學傢中，H.范迪維爾繼續庫默爾的工作，20世紀初到50年代，對費馬大定理進行瞭大量的工作，進一步得到瞭一些使費馬大定理成立的充分條件。還有一些工作是利用大型電子計算機加上精巧的方法來探索費馬大定理。例如1976年，S.S.瓦格斯塔夫證明瞭 p＜ 10 ⁵時，費馬大定理成立。1977年，G.泰雅尼昂用柯召解決不定方程 x ²-1= y ^p的想法，證明瞭 n= 2 p時，若費馬大定理成立，則 2 p| x或 2 p| y。1983年，G.法爾廷斯證明瞭莫德爾猜想，從而推出方程 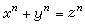，對於給定的 n( n＞3)，僅有有限組非平凡解。

　　卡坦朗猜想　稱α^m為正整數的乘冪，其中α是正整數，m是大於1的整數。E.卡坦朗在1842年猜想：除開8＝2³，9=3²外，沒有兩個連續數都是正整數的乘冪。用不定方程的形式，可寫猜想為：不定方程

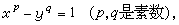(20)

除開 p=2， x=3， q=3， y=2外，沒有其他的正整數解。

　　實際上，可以進一步假定方程（20）中p≠q。q=2的情形，在19世紀早已證明。比較困難的是p=2的情形，直到1962年，柯召給出瞭一個初等而簡練的證明，其證明方法也是富有啟發性的。即他證明瞭不定方程x²-1＝y^p（p＞3是一個奇素數）無正整數解。1961年前後，柯召和J.W.S.卡斯爾斯分別獨立地證明瞭沒有三個連續數都是正整數乘冪這一著名的弱型卡坦朗猜想。R.特艾德曼證明瞭：存在可計算的絕對常數с，方程x^m＝yⁿ+1（x，y，m，n皆≥2）的整數解適合於x^m＜с。近來，還可以算出logloglogс＜1000。

　　當前，不定方程中比較成熟的方法是處理二個變元的不定方程。三個變元以上的高次不定方程，常常是很困難的。1960年，柯召和卡斯爾斯分別獨立地證明瞭不定方程x³+y³+z³=xyz無xyz≠0的整數解，從而證明瞭W.謝爾平斯基認為是很難的一個猜想：不存在三個有理數，它們的和與積都等於1。有的看來很簡單的不定方程，如

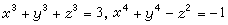等，實際上都不易解決。

　　又如下列這個沒有加減號的不定方程

(21)

P.愛爾特希曾猜想它無整數解。1940年，柯召證明瞭在( x， y)=1時，這一猜想是成立的。同時給出在( x， y)>1時含有一個參數的偶數解。是否存在一組奇數解？迄今尚未解決。另外，C.安德森猜想不定方程

　　 　　　 　(22)

沒有 x＞1， y＞1， z＞1的解。1964年，柯召和孫琦給出瞭方程(22)的無窮多組非平凡解，從而否定瞭這一猜想。

　　

參考書目

　L.J.Mordell，Diophantine Equations，Academic Press，New York，1969.

　柯召、孫琦著：《談談不定方程》，上海教育出版社，上海，1980。

　L.E.Dickson.History of the Theory of Number，Vol.2，Carnegie Institution of Washington，Washington，1920.

　P.Ribenboim，13 Lectures on Fermat's Last Theorem，Springer-Verlag，New York，1980.