分圓域

　　添加單位根到有理數域上而生成的擴域。

　　1847年，E.E.庫默爾宣稱他證明瞭費馬猜想，在證明中，將費馬方程

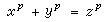（ p為奇素數）在環 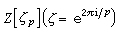中分分解成

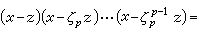
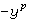，並認為環 Z[ ζ _p]與通常有理數環 Z一樣，每個數都可惟一地表成一些“素數”的乘積。但不久發現他的這個看法是錯誤的，例如在 Z[ ζ ₂₃]中就存在表示成一些“素數”的乘積的方式不是惟一的這種數。於是庫默爾創造瞭“理想數”這一概念來彌補他的證明中的缺陷，並對分圓域的特性作瞭深刻的研究。庫默爾關於分圓域的工作和 C.F.高斯關於二次域的工作，是代數數論的兩個源頭。 J.W.R.戴德金將“理想數”系統化而產生瞭抽象代數中的“理想”這一重要概念。

　　所謂分圓域，是指在有理數域Q上添加n次本原單位根

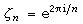（即復平面上單位圓的 n等分點）而得到的數域 K= Q( ζ _n)。由於當 n≡2(mod4)時 Q( ζ _n)= Q( ζ _{n /2})，從而可假定 n扝2(mod4)。和二次域一樣，分圓域中的許多數論特性也比較簡單，例如：

　　對於分圓域K=Q(ζ_n)，K/Q是φ(n)次伽羅瓦擴張，其中φ(n)是歐拉函數，而伽羅瓦群Gal(K/Q)={σα｜1≤α≤n，(α，n)=1}，其中自同構σα是由

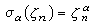所決定的，於是Gal( K/ Q)同構於乘法群

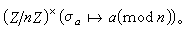
　　K=Q(ζ_n)的整數環為Z[ζ_n]，而判別式為

。

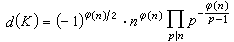　　素數p在分圓域K=Q(ζ_n)中分解規律為：若P籿n，則p為O_K=Z[ζ_n]中g個不同素理想之積，並且每個素理想的剩餘次數均是f，其中f為p對於模n的階數（即f為滿足p^f≡1(modn)的最小正整數），而g=φ(n)/f。若p│n，令

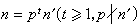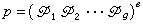，則 ，其中 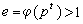（從而 p在 K中分歧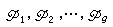）， 是 O _K中 g個不同的素理想，其剩餘次數均為 f， f為 p對於模 n′的階數，而 。

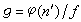　　分圓域K=Q(ζ_n)的單位根群W_K，是由ζ_l生成的l階循環群，其中l=n(當(n≡0(mod4)時)或者l=2n（當n≡1(mod2)時）。

　　分圓域K=Q(ζ_n)的單位群U_K是單位根群W_K和V_K的直積，其中V_K是由

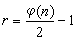個單位 ε ₁， ε ₂，…， ε _r生成的（乘法）自由阿貝爾群，即 K中每個單位均可惟一地表示成 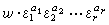，其中 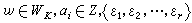稱為分圓域 K的一個基本單位組，尋求分圓域的基本單位組是一個困難的問題。

　　和二次域一樣，分圓域的類數也具有解析的計算公式，但是在公式中包含基本單位組的知識，這使得關於分圓域類數的研究和計算成為困難問題。

　　庫默爾關於分圓域的最重要工作，有以下幾方面：

　　對於每個奇素數p，如果p除不盡分圓域Q(ζ_p)的類數h_p，那麼費馬方程

沒有整數解（ x， y， z）， xyz≠0（例如在100以內，滿足 p| h _p的隻有 P=37、59、67，從而對於不超過100的其他21個奇素數 p，費馬方程 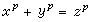均沒有正整數解）。

　　以h

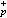表示域 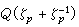(這是 Q( ζ _p)的極大實子域)的類數，則 h 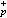｜ h _p，即 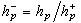為整數，並且

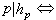
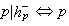除盡伯努利數 B ₂， B ₄，…， B _{p -3}之中某個的分子 。

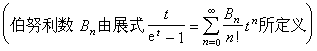　　通過大量的手算，庫默爾發現瞭當p→+∞ 時，h

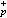變化不大，而 hр則飛速地增長。他猜想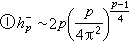： （當P→+∞時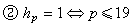）； 。後一猜想由K.烏希達於1971年和J.馬斯利、H.L.蒙哥馬利各自獨立地證明瞭，H.蒙哥馬利還證明瞭對於正整數 n扝2(mod4)則類數為1的分圓域 Q( ζ _n)共有29個，即 n=3，4，5，7，8，9，11，12，1315，16，17，19，20，21，24，25，27，28，32，33，35，36，40，44，45，48，60，84。前一猜想則至今未能解決。

　　繼庫默爾之後，德國數學傢H.哈塞對於分圓域以及一般阿貝爾數域的類數問題作瞭相當精細的研究。他於1952年所著《關於阿貝爾域的類數》就是他的這些研究工作的總結。

　　現代分圓域理論的創始人是巖澤健吉。基於深刻的代數思想和與代數曲線算術理論的類比，他於1959年得到一類數公式：設

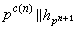(其中 p ^c(n)‖ m表示 p ^c(n)| m，而 p ^l+1籿 m)，則存在與 n無關的常數 μ _p、 λ _p和 v _p，使得當 n充分大時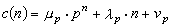， 。他對於更一般的情形也證明瞭類似的公式，例如，對每個代數數域 K，令 h _n是 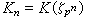的類數， p ^c(n)‖ h _n，則存在與 n無關的常數 μ _p( K)， λ _p( K)和 v _p( K)，使得當 n充分大時，

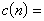
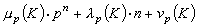。巖澤健吉猜想：對於每個數域 K均有 μ _p( K)=0。他的兩個學生B.費雷羅和L.C.華盛頓於1978年對於阿貝爾數域 K證明瞭這個猜想，但對於其他數域還未完全解決。巖澤健吉還猜想：對於任意全實域 K均有 λ _p( K)=0。這個猜想甚至對於實二次域也未能完全解決。

　　如果l/K是數域的伽羅瓦擴張，並且它的伽羅瓦群是阿貝爾群，那麼l稱為K的阿貝爾擴張。如果K是有理數域Q的阿貝爾擴張，那麼K稱為阿貝爾數域。從伽羅瓦理論可知，分圓域的每個子域都是阿貝爾數域。反之，每個阿貝爾數域也必是某個分圓域Q(ζ_n)的子域，其等價說法是：

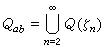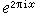是 Q的極大阿貝爾擴域，這就是著名的韋伯-克羅內克定理。對於希爾伯特第12問題：能否對任意的代數數域 K明顯地構作出 K的全部阿貝爾擴張？或者說，能否明顯地刻畫出K的極大阿貝爾擴域？韋伯-克羅內克定理給出瞭關於 K= Q情形的答案。 Q _ab是對 Q添加指數函數(這是單周期函數) 在全部有理點 x∈ Q處的值而得到的域。

　　1853年，20歲的L.克羅內克猜想：每個虛二次域K的極大阿貝爾擴域是將K添加某種橢圓函數（這是雙周期函數）在全部有理點處的取值而得到的域。這就是所謂的克羅內克青春之夢。在1920年高木貞治創立瞭類域論之後，克羅內克猜想得到瞭證明，但是對於其他類型的代數數域，希爾伯特第12問題離完全解決還相距甚遠。

　　分圓域的理論是代數數論中一個在不斷發展的課題。它與模形式理論、代數幾何（特別是橢圓曲線的算術理論）、代數K理論、p進分析等交織在一起，形成當前很活躍的數學領域。

　　

參考書目

　S.Lang，Cyclotomic Fields，Vol.1～2，Springer-Verlag.New York，1978，1980.

　L.C.Washington，Introduction to Cyclotomic Fields，Springer-Verlag，New York，1982.