在研究函數的連續性基礎上產生的一類重要的函數。R.L.貝爾於1899年提出如下的函數分類方法：以區間[0，1]上的函數為例，[0，1]上的連續函數稱為0類函數。0類函數序列點點收斂的極限函數，當它不是0類函數時，就稱為1類函數。1類函數序列點點收斂的極限函數，如果不是0類或1類的函數時，便稱為2類函數。依次對每一個自然數n，可以引入n類函數的概念。如果{fυ}，v=1，2，…，fυ是nυ類函數，{nυ}是自然數列的子序列，{fυ}點點收斂於f(x)，當f(x)不是任何n類函數(n是自然數)，稱f(x)是ω類函數。如此再繼續定義ω+1，ω+2，…類函數。用超限歸納法對一切序數η，都可以定義η類函數。所有這些類的函數統稱為貝爾函數，而貝爾函數的全體稱為貝爾函數類。[0，1]上的狄利克雷函數D（x）（它在有理點上取值為1，無理點上取值為零）不是1類函數，但
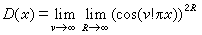，所以
D(
x)是2類函數。可以證明，當序數α＜α
1（α
1是第一個不可列的序數）時，α類是不空的，但α
1類是空集。另外，貝爾函數類的勢（或基數）與[0，1]的勢相等。但[0，1]上所有實函數的勢大於[0，1]的勢。因此定義在[0，1]上的函數中有很多不是貝爾函數。貝爾函數類的另一等價的定義是：包含連續函數全體且對點點收斂的極限運算封閉的最小函數類。
類似地，在n維空間與一般的拓撲空間也可引入貝爾函數類。
波萊爾集 深入討論函數的連續性、可微性、可積性時必不可少的重要集類。設G、F分別表示n維歐幾裡得空間Rn中開集、閉集全體。凡是能表示成G（或F）中一列集{An}的交
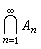(或和
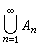)的集的全體記為
G
δ（或
F
σ）。凡能表示成
G
δ（或
F
σ）中一列集{
A
n} 的和
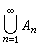（或交
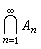）的集的全體記為
G
δσ(或
F
σδ)，如此又繼續可以定義出新的集類
G
δσδ、
F
σδσ，…。同貝爾函數類一樣，對一切序數可用超限歸納法來依次定義新的集類。同樣可以證明：當序數α＜α
1時，上述定義能產生新類型的集，而從α
1開始就不再產生新類型集瞭。由上述方式得到的每個集稱為
R
n上的波萊爾集。波萊爾集全體稱為
R
n上波萊爾集類(也稱波萊爾域)，記為
B(
R
n)。波萊爾集類還有幾種等價的定義：
B(
R
n)是包含
R
n中一切有限“立方體”的最小σ環；
B(
R
n)是包含
R
n中一切開集的最小σ環；
B(
R
n)是包含
R
n中一切閉集的最小σ環。（見
測度論）
在一般拓撲空間中可類似地引入波萊爾集類。
貝爾函數與波萊爾可測函數 設f是拓撲空間X上的實函數，如果對任何實數с，集｛x│f(x)＜с｝是波萊爾集，則稱f是X上的波萊爾可測函數。X上的貝爾函數都是X上的波萊爾可測函數。同樣，設E是X的子集，如果E的特征函數IE(即在E上值為1，E的餘集上值為0的函數)是X上的貝爾函數，則稱E是貝爾集。貝爾集都是波萊爾集。當X=Rn時，波萊爾可測函數（波萊爾可測集）都是貝爾函數（貝爾集）。
解析集 深入研究直線上波萊爾集與勒貝格可測集的關系時發現的重要集類，它們在近代隨機過程中有廣泛的應用。設(Ω，F)是可測空間，E為緊的度量空間，記K(E)×F={A×F是E中的緊集，F∈F}，(K(E)×F)σδ是K(E)×F中的集作可列和後再進行可列交的運算而得到的集類。設B∈(K(E)×F)σδ，稱B在Ω上的投影Ⅱ(B)為Ω中的F解析集。它們的全體記為φ(F)。若用P表示(Ω，F)上的概率測度全體，Fp(p∈P)表示F用p作完全化擴張而得到的σ代數，則利用喬格的容度理論可證明
。
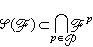特別，當E=Rn，n=1，2…，Ω=[0，1]，F=B[0，1]時，EX[0，1]上的波萊爾集在[0，1]上的投影是解析集，並且φ(F)是[0，1]上勒貝格可測集類的真子集。