群概念的推廣。一集合S稱為半群，是指S的所有元素對於S上的一個二元運算*滿足結合律，即(α*b)*с=α*(b*с)，α、b、с∈S。例如，整數集合對於加法運算是一半群；集合>A的所有子集合組成的集合S(A)對於集合的並，是一半群；集合A上的所有變換T(A)對於變換的乘法，是一半群；集合A上的所有二元關系R（A）對於關系運算的乘法，是一半群。設X是一字符集合，X+是X中的元素組成的有限字符串的集合。若對X+中的兩個元素
、
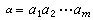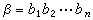定義二元運算*如下：
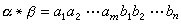，則
X
+對於運算*是一半群，並稱之為由
X生成的自由半群。
對於半群，廣義結合律成立，即在有限個元素相乘時，不論以什麼樣的方式結合，隻要元素排列的次序不變，結果總是相同的。
在半群中，如果對於正整數n定義
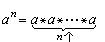，那麼對於正整數
m、
n有
，
。
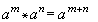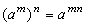若半群中存在元素e，使得對於所有的 α∈S，都有e*α=α，則e稱為半群的左單位元素。同樣可定義半群的右單位元素。如果一半群既有左單位元素，又有右單位元素，那麼這兩個元素必是同一個元素；這個元素稱為半群的單位元素。若一半群中存在元素Z，使得對於所有的α∈S，都有Z*α=Z，則Z稱為半群的左零元素。同樣可以定義半群的右零元素。如果一半群既有左零元素，又有右零元素，那麼這兩個元素必是同一個元素，並稱之為半群的零元素。若半群中的一個元素x滿足條件x*x=x，則x稱為半群的冪等元素。顯然，單位元素和零元素都是冪等元素。
有單位元素的半群，稱為么半群。如果給定的一半群S不含單位元素，那麼可以給它補充一個單位元素e，使它成為么半群S′=S∪{e}，其中S的二元運算*已擴展到S′上，即對所有α∈S，恒有e*α=α*e=α，並且e*e=e。在字符集合X上的字符串半群X+中，可以補上空串，使之成為么半群X
。
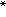如果一半群的元素的個數是有限的，那麼這個半群稱為有限半群。任何有限半群S必含有冪等元素，而且對於任何α∈S，都有一個形式為αk的冪等元素。
如果半群S的二元運算是可交換的，即對於α、b∈S，恒有α*b=b*α，那麼S稱為可交換半群。在可交換半群中，對於正整數n，有
。
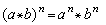如果半群S中存在一個元素α，使得
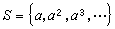，那麼
S稱為由α產生的循環半群，簡稱為循環半群。循環半群顯然是可交換半群。若循環半群的元素個數是無限的，則α的所有冪都是不同的。若循環半群的元素個數是有限的，則存在兩個正整數
r和
m，使得
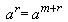，並且
，
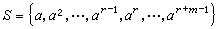r稱為α的瞬態指數，
m稱為 α的周期。如圖
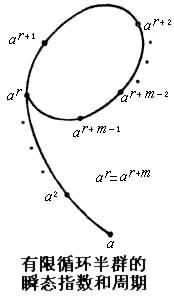有限循環半群的瞬態指數和周期
所示，這時
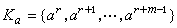是
S的循環子半群。如果
n是
m的倍數，滿足
r≤
n≤
r+
m-1，那麼α
n是冪等元素，且是半群
Kα的單位元素。如果半群
S的一個子集
W對於
S中規定的二元運算而言仍是一個半群，那麼
W稱為
S的子半群。
設S1和S2是兩個半群，f是從S1到S2的一個映射，如果f是保運算的，即對所有的α、b∈S有f(α*b)=f(α)*f(b)，那麼f稱為同態映射。當f為滿射時，則稱S2是S1的同態像。當f是雙射時，則稱f是同構映射。此時就說半群S1和S2是同構的，記為
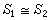。如果
S
2是一個么半群，含有單位元素
e
2，那麼把
S
1中映成
e
2的那些元素組成的集合稱為同態映射f的核，記為Ker(f)。
如果一半群S有單位元素e且有逆，即對於任何α∈S總有元素b使得α*b=b*α=e，那麼半群S是一個群。如果半群S的一個子集A滿足條件
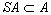，那麼子集
A稱為
S的左理想。同樣可定義右理想。若
A非空且
A≠
S，則稱
A是
S的真理想。若半群
S無真的左理想，則稱
A是左單純的。同樣可定義
S是右單純的。
一個半群是群的充分必要條件為：它既無左真理想，又無右真理想。一個有限么半群是群的充分必要條件為：單位元素是這個半群的惟一冪等元素。
設R是半群S上的一個等價關系，如果對所有的z∈S，當xRy時總有x*zRy*z，那麼等價關系R稱為右不變的。同樣可定義左不變的等價關系。如果半群S上的等價關系R既是左不變的，又是右不變的，那麼R稱為S上的合同關系。
設R是半群S上的合同關系，集合S/R是S在關系R之下的等價組集合，[x]R是S中和x等價的元素組成的等價組。若把等價組之間的二元運算*定義為
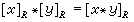，則
S/R是一個半群。設
M
R是如下定義的由
S到
S/R上的映射：
M
R(
x)＝[
x]
R，
x∈
S，[
x]
R∈
S/
R，則
M
R是一個同態映射。
S/R稱為半群
S對於
R的商半群。
近年來，半群的理論在計算機科學中得到瞭應用，引起人們的重視，並成為數學傢和計算機科學傢深入研究的對象，有瞭迅速的發展。
參考書目
E.Hille，Functional Analysis and Semigroups，American Mathematical Society，New York，1948.
A.H.Clifford and G.B.Preston，The Algebraic Theory of Semi groups，American Mathematical Society，Pronidence，Rhode Island，1967.
M.A.Arbib，Theories of Abstract Automata，Prentice Hall，Englewood Cliffs，New Jersey，1969.