最小二乘法

　　測量工作和科學實驗中，根據離散的資料結果尋求其近似函數關係式的一種常用的資料處理方法。由A.-M.勒讓德和C.F.高斯於19世紀初分別獨立提出。

　　設有m個不同的觀測點x₁＜x₂＜…＜x_m及其相應的實驗觀測值y₁,y₂,…,y_m，要求在某選定的函數類中找出一個函數y=f(x)，使它在各結點(觀測點)x_i處所取的值f(x_i)與觀測值y_i的偏差r_i=f(x_i)－y_i的平方和

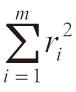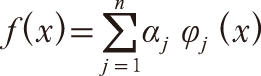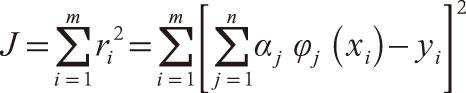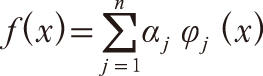達到最小。設已選定函數類的基函數是 φ ₁( x), φ ₂( x),…, φ _n( x)，通常 n% m，取待求函數 f( x)為基函數的線性組合 當 φ _j( x)= x ^j−1時， f( x)為多項式，要求定出系數 α ₁, α ₂,…, α _n使偏差平方和 達到最小。由微分學中的極值原理，可得使 J達到極小的系數 α ₁, α ₂,…, α _n應滿足的線性代數方程組，解該方程組求出系數 α ₁, α ₂,…, α _n，於是就得待求函數 稱上述確定 f( x)的方法為最小二乘法。函數 f( x)是離散數據的近似函數關系式。從幾何意義上講，上述方法等價於確定一給定類型的平面曲線 y= f( x)，使它盡量逼近於實驗數據點，故又稱 曲線擬合。