數論的一個分支，以研究數的有理逼近問題為主。這裏所謂的數是指實數、複數、代數數或超越數。數的有理逼近問題，可表為求某種不等式的整數解問題。由於在整數範圍求解的方程稱為不定方程或丟番圖方程，因而把求不等式的整數解問題稱之為丟番圖逼近。
1842年，P.G.L.狄利克雷首先證明瞭實數有理逼近的一個結果：如果α是任意實數，Q是大於1的實數，那麼存在整數對
。
1891年，A.胡爾維茨將上式改進為
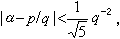並指出，對於某些無理數，常數
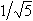是最佳值，不可再減小。但是對於很多無理數，常數
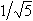不是最佳值，還可再減小。1926年，A.Я.辛欽證明瞭：在勒貝格測度意義下對幾乎所有的實數
α，不等式｜
α-
p/
q｜＜
ψ(
q)/
q的整數解
p、
q有無窮多對還是隻有有窮多對，由級數
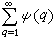是發散的還是收斂的而定，這裡
ψ(
q)(
q＞0)是正的非增函數。此即所謂丟番圖逼近測度定理。例如，對幾乎所有的實數
α和任意的δ>0，不等式｜
α-
p/
q｜＜
q
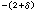隻有有窮多對整數解，而不等式｜
α-
p/
q｜＜
q
-2(
ln
q)
-1有無窮多對整數解。
丟番圖逼近與連分數有密切聯系。一個數的連分數展開，往往就是具體構造有理逼近解的過程。例如，對於任意無理數α，有無窮多個漸近分數pn/qn，滿足不等式
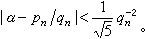
1844年，J.劉維爾開創瞭實代數數的有理逼近的研究，他證明瞭：如果α是次數為d的實代數數，那麼存在一個常數C（α）>0，對於每個不等於α的有理數p/q，有｜α-p/q｜>C(α)/qd。亦即如果μ>d，那麼不等式｜α-p/q｜＜q-μ隻有有窮多個解p/q。根據這一結果，劉維爾構造出瞭歷史上的第一個超越數
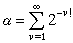。以後一些數學傢不斷改進指數
μ的值，直到得出
μ與
d無關的結果。1909年，A.圖埃得到
μ>1+
d/2。1921年，C.L.西格爾得到
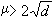。1947年至1948年間，F.戴森和A.O.蓋爾豐德各自獨立證明瞭
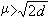。1955年，K.F.羅特得到瞭
μ與
d無關的一個結論：如果
α是實代數數，其次數
d≥2，那麼對於任意的δ>0，不等式
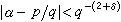隻有有窮多個解。這一結論又稱為圖埃-西格爾-羅特定理。
對於一組數的有理逼近問題，稱之為聯立丟番圖逼近。狄利克雷關於聯立逼近有如下論斷：如果α1，…，αn是n個實數，Q＞1是整數，那麼存在一組整數q，p1，…，pn滿足不等式組
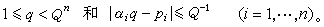進而，如果
α
1，…，
α
n中至少有一個無理數，那麼存在無窮多組解(
p
1/
q，…，
p
n/
q)，適合不等式組
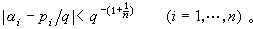
關於實代數數的聯立有理逼近，直到1970年才由W.M.施密特徹底解決。他證明瞭：如果α1，…，αn是實代數數，並且1，α1，…，αn在有理數域上線性無關，那麼對任意的δ>0，隻有有限多個正整數q使得
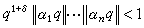成立。式中記號‖
x‖表示
x與最近整數的距離。這一結果的一個等價表達方式：對於上述的實數
α
1，…，
α
n及任意的δ>0，隻有有限多組非零整數
q
1，…，
q
n適合
。
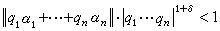由此可知，聯立不等式
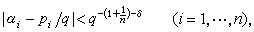隻有有限多組解(
p
1/
q，…，
p
n/
q)，以及不等式
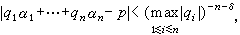隻有有限多組整數解
p，
q
1，…，
q
n。
用代數數逼近代數數，也是丟番圖逼近的一類重要內容。W.M.施密特所著《丟番圖逼近》（1980）一書中，有詳細的論述。
自20世紀以來，丟番圖逼近除自身的發展外，在超越數論、丟番圖方程等方面都有重要的應用。
參考書目
J.W.S.Cassels，An Introduction to Diophantine ApproxiMation，Cambridge Univ.Press，Cambridge，1957.