同一域上兩個向量空間之間的映射,是線性代數的一個主要研究物件。
設V和V′是域K上的向量空間,L是從V到V′的映射,如果對於V中任意向量<u、v以及K中任意元素α、b,有L(αu+bv)=αL(u)+b)L(v),那麼L稱為V到V′的線性變換。例如,解析幾何裡的三維空間中任一向量(x,y,z)在xy平面上的投影:L((x,y,z))=(x,y),就是實數域R上三維向量空間R3到二維向量空間R2的一個線性變換。設x是n維向量,M是m×n實矩陣,令L(x)=M·x,則L就是Rn到Rm的一個線性變換。
設L是V到V′的一個線性變換,B={b)j|j=1,2,…,n}和C={сj|i=1,2,…,m}分別是V和V′的基,於是,V中任一元素x可表為
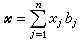 ,其中
x
j是域
K的元素。由線性變換的定義可推得
,其中
x
j是域
K的元素。由線性變換的定義可推得
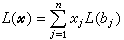 。若
。若
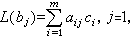
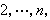 式中
α
ij是域
K的元素,令
M(
L)=(
α
ij),
x寫為列向量(
x
1,
x
2,…
x
n)
T,則
L(
x)=
M(
L)·
x。此時
M(
L)稱為
L對(
B,
C)基的矩陣。當基取定之後,就在
L與
M(
L)之間建立瞭一一對應關系,即
V到
V的一切線性變換與
K上一切
n×
m矩陣之間是一一對應的。線性變換保持子空間及其包含關系,即若
S
1、
S
2都是
V的子空間,且有
式中
α
ij是域
K的元素,令
M(
L)=(
α
ij),
x寫為列向量(
x
1,
x
2,…
x
n)
T,則
L(
x)=
M(
L)·
x。此時
M(
L)稱為
L對(
B,
C)基的矩陣。當基取定之後,就在
L與
M(
L)之間建立瞭一一對應關系,即
V到
V的一切線性變換與
K上一切
n×
m矩陣之間是一一對應的。線性變換保持子空間及其包含關系,即若
S
1、
S
2都是
V的子空間,且有
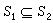 時,則
L(
S
1)、
L(
S
2)必是
V′的子空間,且有
時,則
L(
S
1)、
L(
S
2)必是
V′的子空間,且有
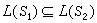 。
V′的零向量在
V中的原像組成的集合,稱為
L的核,記作
Ker
L,
L(
V)表示
V在
L作用下的像,則
Ker
L和
L(
V)分別為
V和
V′的子空間,若以dim
Ker
L和
dim
L(
V)分別表示子空間
Ker
L和
L(
V)的維數,則有
dimKer
L+
dim
L(
V)=
dim
V。dim
Ker
L稱為
L的虧,
dim
L(
V)稱為
L的秩。
。
V′的零向量在
V中的原像組成的集合,稱為
L的核,記作
Ker
L,
L(
V)表示
V在
L作用下的像,則
Ker
L和
L(
V)分別為
V和
V′的子空間,若以dim
Ker
L和
dim
L(
V)分別表示子空間
Ker
L和
L(
V)的維數,則有
dimKer
L+
dim
L(
V)=
dim
V。dim
Ker
L稱為
L的虧,
dim
L(
V)稱為
L的秩。
從線性變換和矩陣的對應關系可知這兩者是同一的,但是線性變換的矩陣與基有關,而線性變換卻不受基的限制,所以線性變換使用起來要方便一些。例如,解齊次線性方程組:
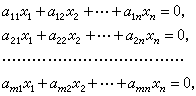 就可看作求
Ker
L的問題,這裡
L是矩陣(
α
ij)所代表的線性變換。因此,當
L的虧為0時方程組隻有零解。在
m<
n時,由虧和秩的關系可知
dim
L(
V)<dim
V,所以,
L的虧>0,此時方程組有非零解,而且所有的解構成
V的一個子空間。於是隻要找出Ker
L的基,就可寫出解的一般表達式。
就可看作求
Ker
L的問題,這裡
L是矩陣(
α
ij)所代表的線性變換。因此,當
L的虧為0時方程組隻有零解。在
m<
n時,由虧和秩的關系可知
dim
L(
V)<dim
V,所以,
L的虧>0,此時方程組有非零解,而且所有的解構成
V的一個子空間。於是隻要找出Ker
L的基,就可寫出解的一般表達式。
在V=V′時,若V到V′的線性變換L是一個雙射,則L稱為可逆變換或非奇異變換。從虧和秩的關系可知以下條件是等價的:①L是正則的;②M(L)是非奇異的;③L(V)=V;④KerV={o}。V的正則變換以映射的合成為運算構成一個群,稱為V上的一般線性群,記作GL(V)。
在V和V′都是賦范線性空間時,V到V′的線性變換就稱為線性算子。如果V′是一維實空間,那麼就把線性算子稱為線性泛函。對於線性算子L若存在常數M,使得‖L(x)‖≤M·‖x‖,對於V的一切x都成立,那麼L稱為有界的。對於線性算子來說,有界和一致連續是等價的。