研究具有廣泛實際背景的一類決策過程的最優化問題。更一般地說,任何最優化問題,隻要具備適當的結構,使得通過某種技巧可以對它建立起動態規劃模型的,都是動態規劃的研究物件。例如,求最短路徑,制訂工業生產中的最優資源使用計畫、最優產品生產計畫,制訂企業管理中的最優庫存方案,水庫調度,化工生產中的最優工藝程序控制,核電站的最優關閉程序控制,航天器的軌道或姿態最優控制等,都是可以應用動態規劃去解決其決策過程最優化問題的實例。所謂決策過程,是指人們在生產和科學實驗活動中中不斷采取決策去控制其演變的過程。利用這類決策過程演變方面的特殊性質,動態規劃發展瞭一套獨特的解決決策過程最優化的方法。這一方法的基礎是動態規劃基本方程和最優性原理。
最初,動態規劃的研究對象在數學上與古典變分法一樣地屬於泛函的極值問題。但古典變分法發展的實際背景是幾何學和力學問題,問題的規模較小,結構較簡單;而動態規劃的背景則是運籌學和控制工程問題,問題的規模較大,結構較復雜。1953年R.貝爾曼總結瞭40年代末期以來對一些決策過程最優化問題的研究,發表專題論文“動態規劃理論導引”,提出瞭動態規劃這一學科名稱,並闡述瞭最優性原理。以後,他以及其他的一些人陸續發表瞭一系列從理論上加以鞏固和從內容上加以充實的論文。1957年,他的專著《動態規劃》一書的出版,標志這一學科的創立。
動態規劃模型 用動態規劃解決決策過程的最優化問題,須先建立該過程的動態規劃模型。實際的決策過程是隨時間而演變的,所以時間參量是模型的一個組成部分。當決策是在離散的時段上采取時,時間參量是離散的,相應的決策過程是離散過程;當決策是在連續的時間上采取時,時間參量是連續的,相應的決策過程是連續過程。例如,在水庫調度中,如果決策是一個時段(一天,一個月等)內的放水量,那麼決策過程是離散的;如果決策是連續的放水流量,那麼決策過程是連續的。在離散情況下,決策過程可劃分成一系列的階段,它也稱為多段決策過程。決策過程從起始到終止的時段數或時間長度稱為歷程。歷程可以是有限、無限或不定。時間參量的集以T表示,對於離散決策過程,它是有限集或可數集。
在決策過程中,狀態起著描述過程的作用,意即所有各個時刻的狀態一經確定,整個過程也就隨之確定。當所有各個時刻如何作出決策的方式給定時,狀態隨時間的演變規律可能是確定性的,也可能是隨機性的,相應的決策過程稱為確定性決策過程或隨機性決策過程。馬爾可夫決策過程就是一種隨機性決策過程。例如,在水庫調度中,水庫蓄水量可取作狀態,若入庫徑流和放水都是確定性的,則相應的決策過程也是確定性的。一個決策過程,如要構成動態規劃模型,其狀態除瞭要起到上述的描述過程的作用外,還須滿足下述的無後效性:給定某一時刻的狀態,在此時刻後過程的發展不受此時刻以前狀態的影響,過程的過去歷史隻通過當前的狀態去影響它未來的發展。在一般情況下,狀態是某一適當定義的狀態集合X中的元素,集X稱為狀態空間。在特殊情況下,它是一個數或向量,稱為狀態變量。
在決策過程中,決策是影響或控制過程發展的外加因素,它是某一適當定義的決策集合U中的元素,集U稱為決策空間。在特殊情況下,它是一個數或向量,稱為決策變量。對於每一給定的t∈T和x∈X,決策必須在U的某一確定的子集U(t,x)內選取,此集稱為時刻t和狀態x下的允許決策集。例如,在水庫調度中,當決策是一個時段的放水量時,U可以是不超過水庫最大蓄水量與最大時段徑流量之和的所有非負實數,U(t,x)可以是不超過t時段水庫蓄水量與徑流量之和的所有非負實數。對於給定的t∈T,給出決策u隨狀態x變化的函數u(t,x),相當於給出根據不同的當前狀態作出不同決策的一套規則,稱為決策規則。決策規則稱為允許的,如它滿足:對所有x∈X,u(t,x)∈U(t,x)。設Ts是與原過程的某一部分過程(或稱為子過程)對應的時間參量集,函數族{u(t,x)|u(t,x)∈U(t,x),t∈Ts}稱為此子過程的允許策略集;特別有,{u(t,x)|u(t,x)∈U(t,x),t∈T}為全過程的允許策略,對歷程有限的離散過程,它是函數序列{u(t0,x),u(t1,x),…,u(tN-1,x)}。如果策略{u(t,x)|t∈T}中的u(t,x)不依賴時間而成為u(x),則稱它為平穩策略,它意味著在任何時刻所選取的決策規則都是相同的。在這種情況下,可以用決策規則u(x)表示策略。
給定時刻t的狀態x和子過程的時間參量集[t,t′](t′>t)上的策略,則對於確定性(隨機性)決策過程,時刻t′的狀態(狀態概率分佈)就完全確定。這種前後狀態與策略的關系,稱為狀態轉移規律。例如,在水庫調度中,設xt是時段t的狀態(時段t開始時的蓄水量),ut是該時段的放水量,gt是該時段的入庫徑流量,xt+1是下一時段t+1的狀態,則有
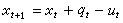 ,此方程表達瞭水庫調度的狀態轉移規律。對於不同類型的決策過程,其狀態轉移規律具有不同的表現形式。對於確定性離散決策過程,它可以由方程
,此方程表達瞭水庫調度的狀態轉移規律。對於不同類型的決策過程,其狀態轉移規律具有不同的表現形式。對於確定性離散決策過程,它可以由方程
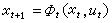 表示,稱為狀態轉移方程,上述水庫例子是它的一個特例。對於隨機性離散決策過程,它可由轉移概率
P
t(
x
t
+1|
x
t,
u
t)表示。對於確定性連續決策過程,它可由含有狀態和決策變量的微分方程表示。對於隨機性連續決策過程,它則可由適當形式的隨機微分方程表示。
表示,稱為狀態轉移方程,上述水庫例子是它的一個特例。對於隨機性離散決策過程,它可由轉移概率
P
t(
x
t
+1|
x
t,
u
t)表示。對於確定性連續決策過程,它可由含有狀態和決策變量的微分方程表示。對於隨機性連續決策過程,它則可由適當形式的隨機微分方程表示。
為瞭對決策過程進行最優化,須先提出衡量過程好壞的準則。在傳統的動態規劃中,此準則是一數量指標,是一定義在原過程和所有子過程上的實值函數,稱為指標函數。例如,對於用於發電的水庫,指標的一種選法是調度過程的總發電量。設此過程由N個時段組成,每一時段t的發電量υt(t=1,2,…,N)為該時段開始時蓄水量xt與該時段放水量ut的函數,則指標函數為
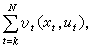 k=1,2,…,
N。對於一般的確定性離散決策過程,此函數的形式為
V(
t,
x
t,
u
t,
x
t
+1,
u
t
+1,…),
t=1,2,…,在動態規劃模型中,要求它滿足下列遞推關系
k=1,2,…,
N。對於一般的確定性離散決策過程,此函數的形式為
V(
t,
x
t,
u
t,
x
t
+1,
u
t
+1,…),
t=1,2,…,在動態規劃模型中,要求它滿足下列遞推關系
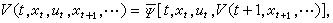 根據問題的不同特點,可以提出形式很不相同的各種指標。例如,對於無限的過程,可以提出無折扣或帶折扣的累計指標,某種意義下的對時間平均的指標等;對於隨機性決策過程,可以提出以
概率、以極值、以
數學期望值或以
方差表示的指標等。
根據問題的不同特點,可以提出形式很不相同的各種指標。例如,對於無限的過程,可以提出無折扣或帶折扣的累計指標,某種意義下的對時間平均的指標等;對於隨機性決策過程,可以提出以
概率、以極值、以
數學期望值或以
方差表示的指標等。
總之,一般說來,決策過程的動態規劃模型包括下列組成部分:時間參量集、狀態空間、決策空間、容許決策集的族、狀態轉移規律、指標、初始和終止條件等。決策過程的最優化,就是要在容許策略集內求出策略,使之能滿足初始和終止條件,並且在某種意義上使指標達到最優值。
動態規劃基本方程 由動態規劃模型的構成可見,作為動態規劃研究對象的決策過程具有如下性質:采用時間與狀態作為參量,它可以形成結構相同的一族決策過程。動態規劃的基本思想就在於從最優化的角度去利用這項性質,把原來的某一決策過程最優化問題,看成采用時間與狀態作為參量的某一族決策過程最優化問題中的一個族元,通過對族的研究得出最優性條件、最優策略和最優過程的結構及其求解方法。換言之,就是把某單一的最優化問題嵌入到具有結構與特征不變的一族最優化問題中去。在這個意義上來說,動態規劃的基本思想是不變嵌入原理的一種特殊形式。動態規劃基本方程就是在這基礎上得出的最優值函數所滿足的方程。這裡最優值函數的定義如下:設t為決策過程的某一時刻,x為該時刻狀態,p[t,tf]是由該時刻起到終止時刻tf止的子過程上的策略,V(t,x,p[t,tf])為此子過程上的指標值,則
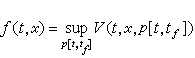
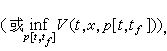 這裡的上(下)確界是在相應的允許策略集內取的。如在此集合內最優策略存在,sup(inf)就變成max(min)。依照決策過程的類型不同,動態規劃基本方程取不同形式,下面列出若幹重要形式:
這裡的上(下)確界是在相應的允許策略集內取的。如在此集合內最優策略存在,sup(inf)就變成max(min)。依照決策過程的類型不同,動態規劃基本方程取不同形式,下面列出若幹重要形式:
① 歷程確定、有限的離散決策過程
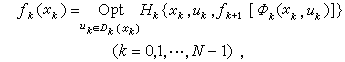 (1)
f
N(
x
N)滿足邊界條件。
(1)
f
N(
x
N)滿足邊界條件。
(1)式中Opt依情況表示sup,inf,max,min;Hk在確定性決策過程中表示指標遞推函數ψ[tk,xk,uk,V]。
② 歷程不定或無限的離散決策過程
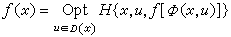 , (2)
f(
x)滿足邊界條件。
, (2)
f(
x)滿足邊界條件。
③ 歷程有限的連續確定性決策過程
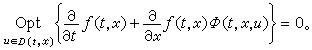 (3)
這裡決策過程的狀態轉移規律由微分方程
ẋ=
φ(
t,
x,
u)確定,指標是終端函數。
(3)
這裡決策過程的狀態轉移規律由微分方程
ẋ=
φ(
t,
x,
u)確定,指標是終端函數。
最優性原理 決策過程的最優策略的基本性質的表述。最初它被用作建立動態規劃理論的基礎。下面是R.貝爾曼原來的表述:不論初始狀態與初始決策為何,對於先前的決策所造成的狀態而言,下餘的那些決策必構成一最優策略,是最優策略具有的性質。在最簡單的問題中,最優性原理的含意和證明都是很簡單的。例如,在最短路徑問題中,可以這樣去理解最優性原理:若由始點S到終點T的最短路徑通過中間點M(見圖
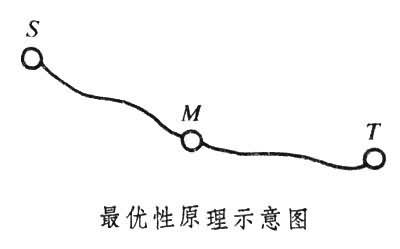 ),則點
M在此路徑所截下的後半段
M
T對於以
M點作為始點的路徑來說必是最短的。否則,就能找到從
M到
T的另一條更短的路徑,把它與原來路徑的前半段
S
M相接,就得到由
S到
T的比原來的路徑更短的路徑,於是得出矛盾。對於復雜的問題,情況自然沒有這樣簡單;在各種不同的決策過程最優化問題中,最優性原理是否成立,必須根據問題的條件進行論證。動態規劃理論的內容之一就是對所建立的各種決策過程的模型論證最優性原理。另一方面,一般說來,最優性原理的成立與動態規劃基本方程的成立並不彼此等價,在許多情況下,可以證明動態規劃基本方程是相應模型的決策過程最優性的充分必要條件,但是從最優性原理本身的表述可見它僅表達策略最優性的必要條件。從實際求解的角度來看,動態規劃基本方程也是更基本的工具。
),則點
M在此路徑所截下的後半段
M
T對於以
M點作為始點的路徑來說必是最短的。否則,就能找到從
M到
T的另一條更短的路徑,把它與原來路徑的前半段
S
M相接,就得到由
S到
T的比原來的路徑更短的路徑,於是得出矛盾。對於復雜的問題,情況自然沒有這樣簡單;在各種不同的決策過程最優化問題中,最優性原理是否成立,必須根據問題的條件進行論證。動態規劃理論的內容之一就是對所建立的各種決策過程的模型論證最優性原理。另一方面,一般說來,最優性原理的成立與動態規劃基本方程的成立並不彼此等價,在許多情況下,可以證明動態規劃基本方程是相應模型的決策過程最優性的充分必要條件,但是從最優性原理本身的表述可見它僅表達策略最優性的必要條件。從實際求解的角度來看,動態規劃基本方程也是更基本的工具。
算法 在動態規劃中最基本的算法是上述方程(1)的數值求解程序,因絕大多數應用問題在構成動態規劃模型後,解析解不存在而須用數值方法求解時,都歸結為此方程的數值求解,這就是所謂的動態規劃常規算法。常規算法的主要困難在於,在方程(1)中對k進行逆推計算時,必須把fk(xk)存於內存中,所需容量與xk的維數成指數增長關系,因而此算法對高維問題是不現實的。目前已提出克服此困難的方法主要有函數逼近法、拉格朗日乘子法、結構分解法、松弛法、狀態增量動態規劃法、微分動態規劃法等,但是困難未獲根本解決。
方程(2)、(3)與(1)不同,它不是函數組的遞推關系,而是單一函數f(x)的函數方程,動態規劃為之提出瞭兩種解法。一是值迭代法,一是策略迭代法。值迭代法中,所謂值是指指標最優值。任選迭代初始的值函數f0(x),對於第n次迭代所得值函數,由下式求第n+1次值函數
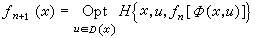 ,
這樣得到兩序列{
f
n(
x)}和{
u
n(
x)},在一定條件下,
n→
,
這樣得到兩序列{
f
n(
x)}和{
u
n(
x)},在一定條件下,
n→
 時,
f
n(
x)→
f(
x),
u
n(
x)→
u
時,
f
n(
x)→
f(
x),
u
n(
x)→
u
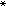 (
x),而
u
(
x),而
u
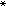 (
x)為最優策略。
(
x)為最優策略。
動態規劃與古典變分法及最大值原理的關系 古典變分法與動態規劃所研究的問題的區別,除背景不同外,前者主要考慮開集的局部極值問題,後者則考慮任何集內的全局極值問題。動態規劃所能處理的極值問題,在約束集和目標函數形式這些方面都可以遠比古典變分法復雜。另一方面,古典變分法的主要結果都可用動態規劃的方法推導出來。例如,在相應的數學模型和古典變分法中通常的假定下,可以證明,動態規劃基本方程(3)就是古典變分法中哈密頓-雅可比方程,而
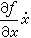 是哈密頓函數。因此方程(3)也稱為哈密頓-雅可比-貝爾曼方程。
是哈密頓函數。因此方程(3)也稱為哈密頓-雅可比-貝爾曼方程。
對於適當構造的數學模型,可以證明,動態規劃裡的指標最優值函數f(x)與Л.С.龐特裡亞金的最大值原理中的哈密頓函數H存在著確定的關系,例如,對於博爾薩問題
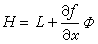 ,其中
L是指標積分內的被積函數,
φ是狀態微分方程
ẋ=
φ的右端部分,其變元應按最優狀態軌線和最優決策取值。而且,動態規劃基本方程正好就是最大值原理中哈密頓函數在容許決策集上取最大值的這一基本條件。
,其中
L是指標積分內的被積函數,
φ是狀態微分方程
ẋ=
φ的右端部分,其變元應按最優狀態軌線和最優決策取值。而且,動態規劃基本方程正好就是最大值原理中哈密頓函數在容許決策集上取最大值的這一基本條件。
簡史 在動態規劃的初步理論建立之後,大部分研究工作是結合運籌學和控制工程兩方面的實際應用而進行的。在確定性問題方面,還對動態規劃與古典變分法的關系以及它與龐特裡亞金的最大值原理的關系進行瞭研究。在隨機性問題方面 ,1960年R.A.霍華德發表瞭“動態規劃與馬爾可夫過程”,1962年和1965年,D.佈克韋爾先後發表瞭“離散動態規劃”和“帶折扣的動態規劃”,這些工作使R.貝爾曼在動態規劃中所開始研究的馬爾可夫決策過程得到重要的發展,使之成為動態規劃的一個分支。
初期,動態規劃的若幹基本方面不夠成熟,隨著理論的發展和應用的需要,對動態規劃的理論基礎的研究逐漸發展,這裡的中心問題包括:最優性原理和動態規劃基本方程的適用范圍及其在動態規劃理論中的地位和作用,建立動態規劃理論的公理化體系的可能性等。基於實際應用的需要,尋找適於在計算機上使用的動態規劃數值計算方法以及與此有關的理論,則是動態規劃研究工作的另一重要方面。在20世紀60年代中後期提出的狀態增量動態規劃、微分動態規劃以及非序列動態規劃的二級最優化問題的研究,都屬於這方面的工作。目前,除上述各方面在繼續發展外,動態規劃還從理論上不斷擴展它的研究領域,例如,在決策方面,已出現把容許決策擴展成廣義函數的工作;在指標方面,則已出現把指標函數擴展成向量指標與其他更一般的非數量指標的工作。
參考書目
R.Bellman,Dynamic Programming,Princeton Univ.Press,Princeton,1957.
R.A.霍華特著,李為政等譯:《動態規劃與馬爾柯夫過程》,上海科學技術出版社,上海,1963。(R.A.Howard,Dynamic Programming and Markov Processes,John Wiley &Sons,New York,1960.)
G.L.Nemhauser,Introduction to Dynamic Program-ming,John Wiley &Sons,New York,1967.
D.J.White,Dynamic Programming,Olive and Boyd,Edinburgh,London,1969.
S.E.Dreyfus and A.M.Law,The Art and Theory of Dynamic Programming,Academic Press,New York,1977.