邏輯的一個分支。有兩個含義：①狹義的歸納邏輯的研究物件是前提和結論之間具有或然聯繫的歸納推理；②廣義的歸納邏輯還包括在進行歸納推理時所使用的科學方法，亦稱歸納法。歸納邏輯按其發展的不同階段，又可以分為古典的歸納邏輯和現代的歸納邏輯兩大類型。
古典類型 歸納邏輯的古典類型主要包括枚舉歸納法、消去歸納法，同時也包括提出和檢驗假說的方法。
S1是 P
S2是 P
…
Si是 P
（S1，S2，…Si不是S類中的全部分子）
所有S是P
枚舉歸納法隻依靠所枚舉的事例的數量，因此，它所得到的結論的可靠程度較低，一旦遇到一個反例，結論就會被推翻。但是，枚舉歸納法仍有一定的作用，通過枚舉歸納法得到的結論可作為進一步研究的假說。
消去歸納法 F.培根所提出的“三表法”和“排斥法”相結合的歸納法，以及J.S.密爾提出的求因果聯系的契合法、差異法（見密爾求因果五法），都是消去歸納法。它們的共同特征是：根據所研究的對象有選擇地安排事例或實驗，然後通過比較消去某些假說，得到比較可靠的結論。以下所說的兩種消去歸納法是用條件句的術語對密爾方法的改進。①假定要探求被研究現象 a的必要條件，推廣密爾的“求同法”，可以先比較a出現的各種場合。如果發現在 a出現的各種場合的先行情況中僅僅有一個共同情況b，那麼b是a的一個必要條件；如果不止有一個共同情況，那麼a可能有幾個必要條件。顯然，在這些場合中的某個場合不出現的情況c不能是a出現的必要條件。如果在先行情況中沒有一個共同情況，這並不意味著a沒有必要條件。在這裡，a的必要條件也許是兩個或兩個以上先行情況的析取。例如，c和d不是各種場合的共同情況，a出現的必要條件也許是“c或者d”的出現。對“c或者d”還可作進一步的分析。上述方法是密爾的契合法的推廣。
② 假定要探求被研究現象 a的充分條件，根據改進過的密爾的“差異法”，可以選擇兩種場合，即正面場合和反面場合。在正面場合中，a出現；而在反面場合中，a不出現。反面場合可以選擇若幹個。然後對幾種場合進行比較。如果僅僅有一個先行情況 b屬於正面場合但不屬於任一反面場合，那麼b是a的一個充分條件；如果有兩個或兩個以上的先行情況屬於所有的正面場合但不屬於任一反面場合，那麼 a可能有幾個充分條件。顯然，在各個反面場合出現的任一先行情況不能是a的充分條件。如果不存在一個先行情況使得正面場合不同於任一反面場合，這並不意味著 a沒有充分條件。因為，a的充分條件也許是兩個或兩個以上情況的合取。例如，c和d是兩種場合中的兩個情況，“c並且d”（但不是它們中的單獨一個）的出現也許是 a出現的充分條件。上述方法是密爾的“差異法”的推廣。
在應用消去歸納法時，充分條件和必要條件可以互相定義。a出現是b出現的必要條件，當且僅當 a不出現是 b不出現的充分條件。例如，施肥是獲得豐收的必要條件，不施肥就是得不到豐收的充分條件。在應用消去歸納法確定被研究現象的條件時，利用這種相互關系可以把①、②兩種方法結合起來使用。
假說方法 假說方法根據一組證據提出一個或一些假說，然後從某一特定的假說演繹出一些結論，這可以寫成蘊涵式："A→B"，接著檢驗這些結論。如果檢驗的結果是：¬B，根據否定式推理：
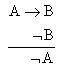就要否定這個假說。如果檢驗的結果是B真，就暫時接受這個假說。這裡應用的是以下形式的歸納推理：
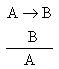接受或排除一個假說的過程是很復雜的，往往不能一次完成。有時，一個假說可以解釋一些現象，但不能解釋另一些現象，在這樣的情況下，就不能簡單地肯定或否定這個假說。一般說來，在兩個或兩個以上的假說中，能解釋的現象數量較大或最大的假說與不能解釋的現象數量之差較大或最大的假說，是可以暫時接受的，它們具有較高程度的可靠性。應用假說方法的過程是一個不斷地提出、檢驗、修改、排除或確定假說過程，在這個過程中，需要應用歸納，也需要應用演繹。例如，科學史上關於光的本性的兩個著名假說“微粒說”和“波動說”，它們都各自能解釋一些光的現象，但又不能完全解釋另一些光的現象，隻具有一定程度的真實性，後來終於被“波粒二象說”（見
波－粒二象性）所取代。
現代類型 19世紀中葉以後，歸納方法的研究和數學裡的概率統計相結合，得到瞭迅速的發展。現代不同的科學領域所應用的歸納方法不盡相同。如在設計科學實驗時用培根、密爾的歸納方法與數理統計相結合的方法，在醫學和經濟學中多應用數理統計。現代歸納邏輯在理論方面的一種發展趨勢，就是用數理邏輯的工具對歸納推理進行系統的、形式化的研究，構造出各種歸納邏輯的公理系統。概率邏輯和模態歸納邏輯就是其中的兩種。
概率邏輯 概率邏輯與數學中的概率統計不同，後者的發展是由於數學和實驗科學的需要；而概率邏輯是由於數理邏輯的發展和研究歸納邏輯的需要。概率邏輯從20世紀20年代開始形成不同的系統，在其發展過程中，R.卡爾納普作出瞭重要貢獻。卡爾納普把歸納推理主要分為5種：①直接推理。這是從總體到樣本的推理。所謂總體是指所考察的一類事物，樣本則是從總體中隨機抽出的若幹個體組成的子類。直接推理的前提是總體中某一性質M出現的頻率，結論是某個樣本中M出現的同樣頻率。
② 預測的推理。這是從一個樣本到另一個不同樣本的推理。
③ 類比推理。即根據兩個個體之間的相似性從一個個體到另一個個體的推理。
④ 逆推理。這是從一個樣本到總體的推理。
⑤ 普遍的推理。這是從樣本到具有普遍形式的假設的推理。
卡爾納普認為，歸納邏輯是關於歸納推理的理論，是以概率的概念為基礎的，歸納邏輯就是概率邏輯。概率是一組命題即某些給定的證據和另一個命題即假設之間的關系，也就是證據對假設的確證度，卡爾納普稱之為概率1，以便與相對頻率即概率2相區別。設證據為e，假設為 h，確證度q=c(h，e)，c稱為確證函數或c函數。卡爾納普利用數理邏輯和語義學的方法，構造瞭一個以研究確證度為對象的概率邏輯系統，並對他所提出的5種歸納推理作瞭概率的處理。
模態歸納邏輯 在概率邏輯發展之後，20世紀中葉以來，有的學者如美國的P.J.科恩用模態邏輯作為處理歸納推理的工具。科恩指出，卡爾納普的概率邏輯面臨不少困難，對歸納推理不宜作概率處理。他所提出的歸納邏輯的研究對象是證據e對假設h的支持度，用s(h，e)表示，s稱為支持函數。在他看來，支持度可列為不同的等級，不同等級的支持度，就是證據給予假設不同等級的必然性，一個被證明瞭的理論就是由較低級的必然性達到較高級的必然性。不同等級的支持度是廣義模態邏輯的研究對象。科恩證明瞭一個廣義模態邏輯系統滿足他的支持函數的全部要求。
現代歸納邏輯正處在深入研究的新階段，它與現代形式邏輯即數理邏輯的一些分支，以及與信息論、模糊數學和人工智能等學科密切結合、相互滲透，並以這些學科為工具，不斷地開拓新的領域。
參考書目
J.S.Mill，A System of Logic，8th.ed.，London，1872.
R.Carnap，Logical Foundations of Proda dility，Chicago，1950.
L.J.Cohen，The Implications of Induction，London，1970.