應用於生物學中的數理統計方法。即用數理統計的原理和方法,分析和解釋生物界的種種現象和資料資料,以求把握其本質和規律性。
發展簡況 最早提出生物統計思想的是比利時數學傢L.A.J.凱特萊,他試圖把統計學的理論應用於解決生物學、醫學和社會學中的問題。1866年,G.J.孟德爾揭示瞭遺傳的基本規律,這是最早運用數理統計於生物實驗的一個成功的範例(見孟德爾定律)。1889年,F.高爾爾頓在《自然的遺傳》一書中,通過對人體身高的研究指出,子代的身高不僅與親代的身高相關,而且有向平均值“回歸”的趨勢,由此提出瞭“回歸”和“相關”的概念和算法,從而奠定瞭生物統計的基礎。高爾頓的學生K.皮爾遜進一步把統計學應用於生物研究,提出瞭實際測定數與理論預期數之間的偏離度指數即卡方差(x2)的概念和算法,這在屬性的統計分析上起瞭重要作用。1899年,他創辦瞭《生物統計》雜志,還建立瞭一所數理統計學校。他的學生W.S.戈塞特對樣本標準差作瞭許多研究,並於1908年以“Student”的筆名將t-檢驗法發表於《生物統計》雜志上。此後,t-檢驗法就成瞭生物統計學中的基本工具之一。英國數學傢R.A.費希爾指出,隻註意事後的數據分析是不夠的,事先必須作好實驗設計。他使實驗設計成瞭生物統計的一個分支。他的學生G.W.斯奈迪格把變異來源不同的均方比值稱為F值,並指出當F值大於理論上5%概率水準的F值時,該項變異來源的必然性效應就從偶然性變量中分析出來瞭,這就是“方差分析法”。上述這些方法對於農業科學、生物學特別是遺傳學的研究,起瞭重大的推動作用,20世紀20年代以來,各種數理統計方法陸續創立,它們在實驗室、田間、飼養和臨床實驗中得到廣泛應用並日益擴大到整個工業界。70年代,隨著計算機的普及,使本來由於計算量過大而不得不放棄的統計方法又獲得瞭新的生命力,應用更為廣泛,並在現代科技中占有十分重要的地位。
個體與總體參數 一個觀測對象(如一個7歲男孩)的某些性狀(如身高等)的量度結果,稱為一個個體。來源相同的各個個體(如各個7歲男孩的身高值)之間的差異稱為個體變異。總體是通過統計所欲瞭解的對象,其中的個體可以是有限的也可以是無限的。觀測數據可以是計數的(離散的)(如單位面積中的昆蟲數),也可以是計量的(如身高、體重、血壓、肺活量等)。總體最基本的參數有兩類:表示水平的稱為位置參數或型值,如平均數、中位數、率等;反映個體差異大小的稱為分散度參數,如標準差、極差等。總體參數是一個客觀存在但通常卻又是未知的常數。隻能用樣本去估計它。這樣做自然會有誤差。
樣本平均數,即
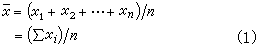
其中xi表示第i個個體的觀測值;n為樣本中的個體數,稱為樣本大小;∑為求和號,∑x表示x的合計。凡是從樣本計算出來的數值都稱為統計量,它是對相應的總體值的一種估計。例如x是總體均數μ的一種估計。若總體均數x正好等於μ,則稱x為μ的無偏估計,意謂用x估計μ雖有誤差但平均來說是無偏的。此時又稱μ為x的期望,記作
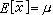 。
。
率 反映事物或現象出現的機會或頻度,常用百分率或小數表示。如:感染率、死亡率、男嬰率等。若以P代表陽性率,則陰性率Q=1-P。若將男嬰記作x=1,女嬰記作x=0,則n個嬰兒的性別指標的均數x=(∑x/n=P就是男嬰率。可見,率可以看成是個體取值為1或0的計數數據的均數。這種樣本的率P也是對應的總體率P的無偏估計。總體的率又稱為概率。
中位數 是數據按大小排列後位於中央的數值。對於分佈不對稱的指標(如機體內、外環境中的有害物質濃度等)往往會有少數特大值,此時,中位數比均數更具代表性,也更穩定。當n為偶數時,則取中央兩數的均數。
眾數 即最常出現的數值。如正常妊娠天數的眾數為280天。
極差 即最大值與最小值之差。是用於表示數據分散度的簡單指標。
方差 比極差更全面地反映個體差異的大小。若總體中有N個個體,則總體的方差為
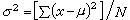 (2)
(2)
樣本方差
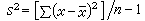 (3)
(3)
是總體方差的無偏估計。若(3)式的分母改用n,就不是無偏估計。n-1是自由度:樣本中有n個獨立的觀測指標x,它們都是隨機變量,它們對於總體均數的離差平方和∑(x-μ)2,是n個獨立隨機變量之和,稱為有n個自由度;而(3)式中的∑(x-x)2,是用x代替瞭μ,等於對n個x的值加瞭一個限制,即∑x必須等於nx,換言之,∑(x-x)2隻相當於n-1個獨立的隨機變量之和,所以它隻有n-1個自由度。一般地說,對統計量每加上一種限制就用去瞭一個自由度。為瞭運算上的方便,離均差平方和有時也記作:
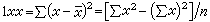 (4)
(4)
標準差 是方差的平方根。它和觀測值有相同的單位。是最常用的表示數據分散程度的指標。對於正態分佈的數據,它的用處尤大。樣本標準差s是對總體標準差σ的一種估計。s的值可在有統計功能的計算器上直接得出。計算s值的功能鍵常用
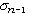 表示。
表示。
變異系數 即
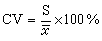 (5)
它是不受單位影響的量,可用於比較兩種單位不同的指標(如生物體的長度與重量)的個體變異大小。例如,三隻小白鼠的體重
x=22,24,27(克)。它們的均數
(5)
它是不受單位影響的量,可用於比較兩種單位不同的指標(如生物體的長度與重量)的個體變異大小。例如,三隻小白鼠的體重
x=22,24,27(克)。它們的均數
x=(22+24+27)/3=24.3(克)
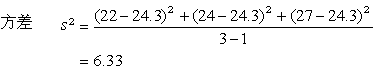
標準差
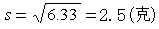
變異系數
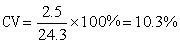
極差 Δx=27-22=5(克)。中位數是24克。
概率 表示客觀事物可能發生的程度。它是實際觀察到的率(如男嬰率)的總體均值或期望值。它的通用符號是P。常用小數或分數表示其大小。例如用0《P《1表示概率的取值范圍為0~1:假定P(男嬰)=22/43=0.512表示生男嬰的概率為22/43或0.512,即略大於1/2。這一理論值是根據反復多次的大樣本統計結果歸納出來的。概率可以從量的方面來說明總體的性質。所謂“小概率事件”是指實際上不大可能發生的事件。
為充分地瞭解一個總體,就須知道個體的取值范圍,以及出現的各種可能值的概率,即概率分佈,簡稱分佈。
正態分佈 一種理想的對稱型分佈。有些生物學指標遠非正態分佈,而是呈左右不對稱的所謂偏態,但當樣本增大時,它們的均數卻趨向正態分佈。這一性質有重要的實用價值。
直方圖 一種根據頻數表繪制的圖,它以橫軸上的長方形的面積表示各組的頻數,長方形在橫軸上的邊長相當於組距(圖1)。
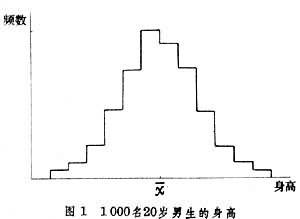
如果一步步地縮小直方圖的組距,同時增大樣本含量,最終將要趨於圖2那樣的極限。在圖2中,曲線以下橫軸以上的面積表示概率,這種曲線稱為“(概率)分佈曲線”。
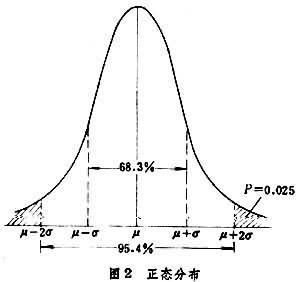
正態分佈具有以下性質:以總體均數μ為中心,在中心處的分佈曲線最高;兩側與μ距離相等的對稱區間的上方有相同的面積(概率);與μ相距愈遠的區間的概率愈小;可以用μ與σ(總體標準差)這兩個參數來描述整個分佈(圖3)。
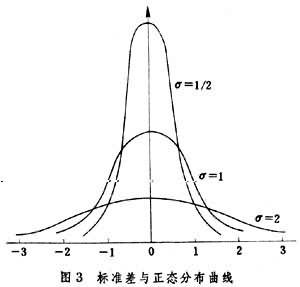 隻要知道瞭
μ和
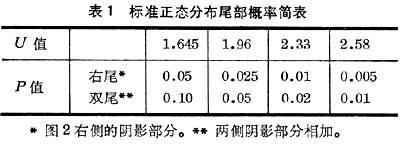
σ,則個體落入任何區間的概率均可從(統計學書上)事先算好的正態分佈表中查得。表1是這種表的一個摘要。
表1 標準正態分佈尾部概率簡表
隻要知道瞭
μ和
σ,則個體落入任何區間的概率均可從(統計學書上)事先算好的正態分佈表中查得。表1是這種表的一個摘要。
表1 標準正態分佈尾部概率簡表
標準正態分佈 凡是正態分佈的數據,均可通過減去均數並除以標準差而使之成為均數為0、標準差為1的標準正態分佈。經過這種變換的指標記為U,
 (6)
x遵從均數為
μ標準差為
σ的正態分佈,通常以簡單的符號來表示:
x~
N(
μ,
σ)。故可用
U~
N(0,1)表示“
U遵從標準正態分佈”。這種分佈很常用,尤其是表1所列幾個界限值。
(6)
x遵從均數為
μ標準差為
σ的正態分佈,通常以簡單的符號來表示:
x~
N(
μ,
σ)。故可用
U~
N(0,1)表示“
U遵從標準正態分佈”。這種分佈很常用,尤其是表1所列幾個界限值。
當樣本含量增大時,不論原始數據是不是正態分佈,它的大多數統計指標均趨向正態分佈,從而可以進一步化為標準正態分佈,再根據μ的界值來作出推斷(表1)。
正常范圍 生物界的正常范圍常用於診斷、鑒別和分類。制定正常范圍需要一些先決條件:原始數據必須來自同一總體;樣本對總體的代表性要好;儀器、試劑和方法都沒有偏性。理想的界限應有較高的靈敏度與特異度。前者是對異常者的識別率=1-假陽性率;後者是對正常者的識別率=1-假陰性率。當尚未掌握異常者的情況時,可暫將特異度定在0.95(即95%的正常者為此范圍所覆蓋)的水平;待掌握瞭異常者的數據分佈後,再酌情修改界限以便兼顧靈敏度與特異度這兩個方面。
抽樣 為瞭估計總體的參數(如均數、率、標準差等)而從其中抽出一部分個體組成供分析的樣本稱為抽樣。抽樣方法應能防止主、客觀因素造成偏性(即系統誤差),保證樣本對總體的代表性。簡單隨機抽樣是以抽簽或相當於抽簽的方式從總體中抽取個體組成樣本。其要點是:總體中每個個體被抽中的機會必須均等。系統抽樣是將總體劃分為時間或空間順序相等的n個部分,再機械地取每一部分的第K個個體組成樣本,K是一次隨機抽定的。例如,欲抽查十分之一學生的成績,可從0到9這10個整數中隨機地抽定一個數,假設為3,則凡學生證號最後一個數是3者均為被抽中的對象。分層抽樣是事先將總體分為不同的層次(如地區、年齡、性別等),再分別從各層次中按適當比例抽樣。用此法可以從層間差異較大的總體中獲取代表性較好的樣本。整群抽樣是以群體為單位進行抽樣,凡抽中的單位就全面調查。此法便於實施,但抽樣誤差較大,一般不可沿用基於簡單隨機抽樣的普通公式計算抽樣誤差。此外,還可以分階段地、混合地使用上述方法。如兩階段抽樣、多階段抽樣、分層整群抽樣、多階段等概率抽樣等。
用樣本統計量去估計總體參數難免會有抽樣誤差,它的大小與個體變異(標準差)的大小成正比;與樣本含量的平方根成反比。表示抽樣誤差大小的統計指標是標準誤
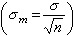
或代以統計量
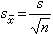 (7)
相當於將每一個樣本(設想有許多來自同一總體的樣本)的均數
x(或率
P)看成為一個個體時的標準差,它反映瞭取自同一總體的不同樣本之間的差異。(7)式適用於簡單隨機抽樣和系統抽樣。其他幾種抽樣方法的算式較繁。
(7)
相當於將每一個樣本(設想有許多來自同一總體的樣本)的均數
x(或率
P)看成為一個個體時的標準差,它反映瞭取自同一總體的不同樣本之間的差異。(7)式適用於簡單隨機抽樣和系統抽樣。其他幾種抽樣方法的算式較繁。
差異的顯著性 兩個或兩組數據相比,總會有或大或小的差異。問題是這種差異僅僅是抽樣誤差的反映呢還是由於它們來自不同的總體?即是否存在著實質性差異?用統計學的術語來說,就是要判斷數據間的差異是否“顯著”。用統計方法來推斷差異的性質稱為差異的顯著性檢驗。顯著性檢驗的方法很多,基本步驟大體如下:先假定數據均來自同一總體,即假設要比較的數據並無實質性差異,稱為零假設;根據原始數據計算因抽樣誤差而出現此種程度差異的概率P;若P甚小,則根據“小概率事件實際上不大可能發生”這一原理否定零假設,認為“差異顯著”,即這種差異從統計學的角度來看是有意義的;反之,若P不算小,就不否定零假設,認為“差異不顯著”,即不能排除抽樣誤差范圍內的波動。正確地運用顯著性檢驗,可使實驗或調查的結論建立在更科學、穩妥的基礎之上,避免簡單化和絕對化。
顯著性水準 概率的大小隻能相對而言,在生物學數據的差異顯著性檢驗中,已習慣用α=0.05為小概率的上限。有時,為嚴格起見,也規定α=0.01。稱α為顯著性水準,它是當零假設正確時卻錯誤地將其否定(第Ⅰ類錯誤)的概率。但也不是α定得愈小愈好。倘若零假設是不對的卻未能否定,它(第Ⅱ類錯誤)的概率β將因α規定得愈小而愈大。增大樣本可以減小出現第Ⅰ或第Ⅱ類錯誤的概率。
兩個計數數據的比較 最簡單的差異顯著性檢驗是比較按零假設系“來自同一總體”的兩個計數a與b。
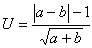 (8)
U服從標準正態分佈。換言之,
U>1.96的概率
P<0.05(表1)。
(8)
U服從標準正態分佈。換言之,
U>1.96的概率
P<0.05(表1)。
例如,用“714”試治喘息型氣管炎,與用氨茶堿進行比較:在每名患者身上交替使用這兩種藥各一療程。半數患者先服甲藥,另一半先服乙藥。結果16名患者用氨茶堿效果較好(a=16),5名用“714”較好(b=5)。
將上述結果代入(8)式
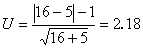 因
U>1.96,
P<0.05,故否定零假設,因此可以認為兩藥的療效並不相同,即“714”的療效不及氨茶堿。
因
U>1.96,
P<0.05,故否定零假設,因此可以認為兩藥的療效並不相同,即“714”的療效不及氨茶堿。
凡用標準正態分佈統計量U進行的顯著性檢驗,均可稱為U檢驗。
兩個均數的比較 也可用U檢驗:
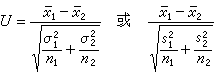 (9)
(9)
其中x1、s1和n1分別表示第1個樣本的均值、標準和含量,餘類推。σ2為總體方差,通常是未知的,故常用右邊的近似式。當兩樣本的含量n1+n2=n<25時,(9)式的近似程度欠佳,最好用t檢驗。
t檢驗是根據統計量t的概率分佈(稱為t分佈,見表2而進行的顯著性檢驗。
表2 禾苗噴霧後凈增長度(cm)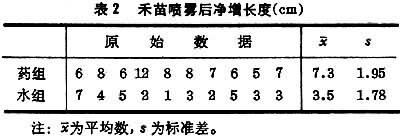 比較兩個均數時,
比較兩個均數時,
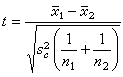 (10)
(10)
其中s02為合並的方差,即
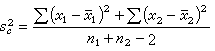
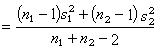 (11)
(11)
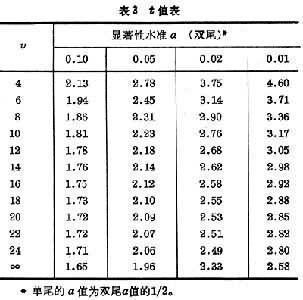
其中x1表示第1個樣本中的數據,x2表示第2個樣本中的數據,其餘符號意義同前。自由度υ=n1+n1-2。用
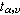 表示顯著性水準為
α、自由度為
υ的
t臨界值,可從表3中查得。若按(10)式算得的
t的絕對值大於
表示顯著性水準為
α、自由度為
υ的
t臨界值,可從表3中查得。若按(10)式算得的
t的絕對值大於
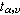 ,則
P<
d,有顯著性差異。
,則
P<
d,有顯著性差異。
例如,在一塊小區田裡選20兜長勢均勻的禾苗作試驗,隨機抽取其中10兜噴以粗制“920”溶液,其餘噴水作對照。三日後,測量禾苗凈增長度,結果如表2。
由(11)式
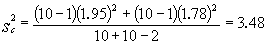 代入(10)式
代入(10)式
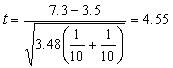 查表3,當
α=0.01,
υ=10+10-2=18,
t
0.01,18=2.88;此例
t=4.55>2.88,
p<0.01,有顯著性差異。 結論:粗制“920”有加速禾苗生長的作用。
表3 t值表
查表3,當
α=0.01,
υ=10+10-2=18,
t
0.01,18=2.88;此例
t=4.55>2.88,
p<0.01,有顯著性差異。 結論:粗制“920”有加速禾苗生長的作用。
表3 t值表
兩個率的比較 當樣本較大,以致兩個樣本的陽性數、陰性數都大於5時,可用U檢驗:
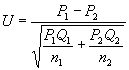 (12)
P
1、
Q
1和
n
1,分別表示第1組的陽性率、陰性率和含量,餘類推。若應用
U檢驗的上述條件不能滿足,可用近似程度較好的
t檢驗:
(12)
P
1、
Q
1和
n
1,分別表示第1組的陽性率、陰性率和含量,餘類推。若應用
U檢驗的上述條件不能滿足,可用近似程度較好的
t檢驗:
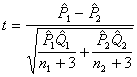 (13)
其中
(13)
其中
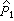 =(
a
1+1)(
n
1+2),
a
1是第1組的陽性數,
=(
a
1+1)(
n
1+2),
a
1是第1組的陽性數,
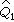 =1-
=1-
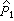 ,餘類推。自由度
υ=
n
1+
n
2-2。
,餘類推。自由度
υ=
n
1+
n
2-2。
例如,甲組n1=23,其中兩個呈“+”反應,乙組n2=77,全為“-”反應。現在來檢驗差異的顯著性。
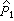 =(2+1)/(23+2)=0.120,
=(2+1)/(23+2)=0.120,
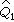 =1-0.120=0.880;
=1-0.120=0.880;
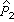 =(0+1)/(77+2)=0.013,
=(0+1)/(77+2)=0.013,
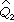 =1-0.013=0.987。代入(13) 式得
t=1.65,
υ=23+77-2=98,接近100,由表3知
=1-0.013=0.987。代入(13) 式得
t=1.65,
υ=23+77-2=98,接近100,由表3知
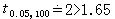 ,
P>0.05,故無顯著性差異。
,
P>0.05,故無顯著性差異。
置信限 由樣本估計總體,難免會有抽樣誤差,這就產生瞭統計量的可信程度和可信范圍的問題。如果我們將統計量x(或P)看成為一個個體,x的總體均數為μ,標準差為σm=σ/
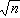 ;而且不論
x的分佈是否正態,隻要
n不是很小,
x就近似正態分佈,亦即
U=(
x-
μ)/
σ
m近似標準正態分佈。於是下式
;而且不論
x的分佈是否正態,隻要
n不是很小,
x就近似正態分佈,亦即
U=(
x-
μ)/
σ
m近似標準正態分佈。於是下式
 (14)
成立的概率為0.95。用
S
x代替其中的
σ
m,稍作變換,即得由樣本統計量
x和
S
x來估計總體參數
μ的一個區間(范圍):
(14)
成立的概率為0.95。用
S
x代替其中的
σ
m,稍作變換,即得由樣本統計量
x和
S
x來估計總體參數
μ的一個區間(范圍):
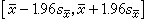 (15)
這一區間的實際計算值隨樣本而異,但它們覆蓋
(15)
這一區間的實際計算值隨樣本而異,但它們覆蓋
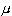 的機會──稱為置信水準──是95%,所以稱(15)式為95%置信區間,它的上、下限就是置信限。
的機會──稱為置信水準──是95%,所以稱(15)式為95%置信區間,它的上、下限就是置信限。
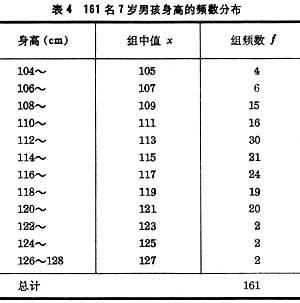
例如按表4中數據可算出161名7歲男孩的身高均值x=115.01(厘米),標準差s=4.63,標準誤由(7)式得
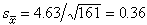 。由(15)式得7歲男孩身高總體均數
μ的95%置信限為[114.95,115.73]。
表4 161名7歲男孩身高的頻數分佈
。由(15)式得7歲男孩身高總體均數
μ的95%置信限為[114.95,115.73]。
表4 161名7歲男孩身高的頻數分佈
兩總體均數之差μ1-μ2的置信限可按下式計算:
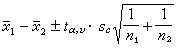 (16)
式中符號意義同前。當置信水準(1-
α)為95%時,
α=0.05;
υ=
n
1+
n
2-2;據此,從表2中即可查出
(16)
式中符號意義同前。當置信水準(1-
α)為95%時,
α=0.05;
υ=
n
1+
n
2-2;據此,從表2中即可查出
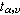 的值。
的值。
方差分析 也是基本的統計分析方法之一,較常用於分析實驗數據。用於檢驗多組均數間差異的顯著性和多因素的單獨效應與交互影響的顯著性等。基本思路:正態分佈數據的變差,可分為未能控制與未能解釋的“誤差”和來源明確與能夠解釋的“效應”這兩大部分。後者還可以進一步劃分成各種不同因素及其交互影響所引起的效應。
按一個因素的不同水平分組的數據結構:
觀測值=平均效應+該水平(組)效應+誤差 (17)
當檢驗 K組數據間的差異顯著性時,零假設相當於“各組效應均為零”;當零假設被否定時備選假設相當於“在 K種處理(水平)中至少有一種的效應不為零”。一般用離均差平方和(記作SS)來衡量數據間的變異,再除以自由度(υ)則稱為均方,記作MS=SS/υ,它反映瞭平均的變異程度。設每組各有n個數據,則K組共有N=nK個。它們的總變異
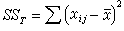 ,
x
ij表示第
i組的第
j個數據;各組之間的變異
,
x
ij表示第
i組的第
j個數據;各組之間的變異
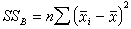 ,
x
i是第
i組的均數;組內變異(即誤差)
,
x
i是第
i組的均數;組內變異(即誤差)
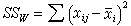 。三者之間有以下關系:
。三者之間有以下關系:
SST=SSB+SSW (18)
它們的自由度也同樣可加:(nK-1)=(K-1)+(nK-K) (19)
組間均方 M S B= S S B/( K-1)與組內均方 M S W= S S W/( n K- K)之比F=MSB/MSW (20)
可用來檢驗組間差異的顯著性。 F的界值可從 F值表中查得。用於方差分析的軟件可以打印出包含 F及相應的尾部概率 P值的表格(表6)。 表6 表5中數據的方差分析表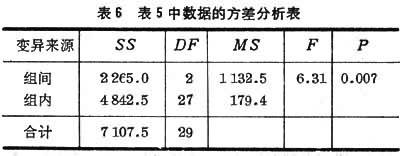
例如將30名收縮壓在200毫米汞柱左右的高血壓患者隨機分為3組,每組各用一種藥物,一個療程後測血壓,結果如表5。
表5 三組病人用藥後的血壓(mmHg)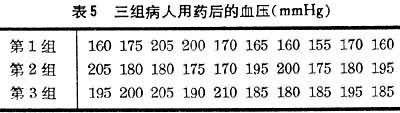
利用現成的計算機軟件打印的結果如表6。表中P<0.01,表明組間有顯著性差異。DF即自由變。
按兩個因素分組的數據結構:
觀測值=均數+行效應+列效應+交互影響+誤差 (21)
其中“均數”指平均效應,行效應指按第1因素分組的組效應,列效應指按第2因素分組的組效應。交互影響的含義:當數據按兩個以上的因素分組時,如果這些因素的效應並不是彼此獨立的,即一個因素的效應隨另一因素的水平不同而異,則稱這兩個因素之間存在著交互影響。例如在三種病型的患者身上試用4種藥物後的血壓改變如表7所示。其中每個數據代表一個病人的用藥結果。
表7 原始數據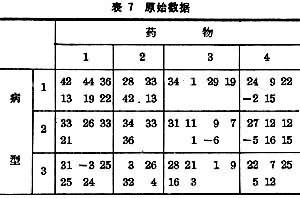
表8是計算機給出的結果。
表8 方差分析表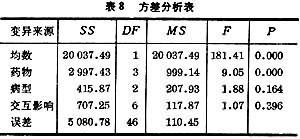
從P值可以看出:三種病型之間無顯著性差異;藥物間有顯著性差異;藥物與病型的交互影響無顯著性。“均數”除非來源於配對數據之差或兩均數之差,一般都是有顯著性的,即不為零。
隻有進行瞭重復實驗,即兩因素的各種不同水平的搭配均有兩個以上數據,才有可能算出交互影響項的變異。這是在設計時應該想到的。
上述內容不難推廣到三個以上因素的方差分析。
理論的驗證──x2檢驗 生物科學註重實驗、調查。歸納得來的理論、演繹得來的假說,還須經過實踐來驗證。由於個體差異大是生物學數據的固有特點,所以這種驗證也隻能是統計的。
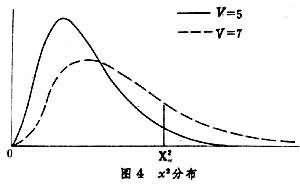
統計量x2 是V個獨立標準正態分佈統計量的平方和,它的分佈與自由度V有關(表9,圖4)。
 x
2在生物學研究中用處很大,常用於衡量某種理論與實際計數的吻合性,或按兩種指標分組的列聯表的獨立性。實際觀察到的分配在表中每個小格裡的計數數據,可以假定是服從泊松分佈規律的數據──它的特點是方差等於平均數,且當樣本不很小時,近似於正態分佈。由此可以理解下列這個常用的基本公式。
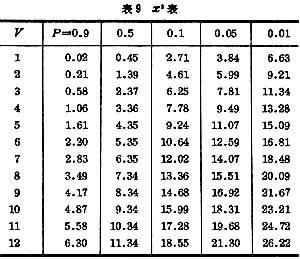
表9 x2表
x
2在生物學研究中用處很大,常用於衡量某種理論與實際計數的吻合性,或按兩種指標分組的列聯表的獨立性。實際觀察到的分配在表中每個小格裡的計數數據,可以假定是服從泊松分佈規律的數據──它的特點是方差等於平均數,且當樣本不很小時,近似於正態分佈。由此可以理解下列這個常用的基本公式。
表9 x2表
x2=
 (22)
其中的理論數可按欲檢驗的生物學理論或零假設計算,自由度
V=
x
2中蘊含獨立統計量的個數。對於普通的隻有一行
K格的單向表──1×
K表,因受合計的約束,
(22)
其中的理論數可按欲檢驗的生物學理論或零假設計算,自由度
V=
x
2中蘊含獨立統計量的個數。對於普通的隻有一行
K格的單向表──1×
K表,因受合計的約束,
V=K-1
而雙向的有 r行 c列的 r× c表,則因受行合計與列合計的約束,V=(r-1)(c-1)
對計算結果的分析可參照差異的顯著性檢驗。例如番茄的真實紫莖、缺刻葉植株AACC與真實綠莖、馬鈴薯葉植株aacc雜交,子2代得如下結果(株數):
紫莖缺刻葉 紫莖馬鈴薯葉 綠莖缺刻葉 綠莖馬鈴薯葉
247 90 83 34
上述觀察頻數是否與遺傳學的獨立分配定律的理論比例:9:3:3:1相符,可用 x 2分佈來衡量實驗觀察結果與理論頻數之間的吻合度。將上述理論比例改為構成比即: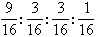 或0.5625:0.1875:0.1875:0.0625子2代總株數為247+90+83+34=454;理論頻數是總株數與構成比的乘積,故得255.375:85.125:85.125:28.375,代入(22)式:
或0.5625:0.1875:0.1875:0.0625子2代總株數為247+90+83+34=454;理論頻數是總株數與構成比的乘積,故得255.375:85.125:85.125:28.375,代入(22)式:
x2=
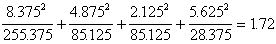 自由度
V=4-1=3,查表9,
自由度
V=4-1=3,查表9,
 =2.37>1.72,故
P>0.5,高度吻合。衡量吻合度不能用小樣。
=2.37>1.72,故
P>0.5,高度吻合。衡量吻合度不能用小樣。
列聯表 即按兩種指標分成r行c列的所謂r×c表,常用於衡量指標間的聯系或獨立性,為此亦可用(22)式。
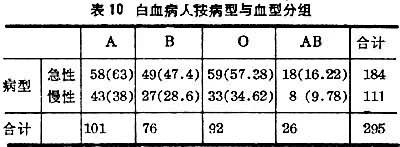
例如根據表10中數據分析血型與白血病病型間有無聯系。零假設是“二者沒有聯系”。括號中數據是根據零假設計算的理論頻數=行合計×列合計÷總計。代入(22)式得x2=1.84,V=行數-1×列數-1=(2-1)×(4-1)=3。查表3,
 =2.37>1.84,
P>0.5,故不能否定零假設。即不能認為血型與白血病病型有聯系。
表10 白血病人按病型和血型分組
=2.37>1.84,
P>0.5,故不能否定零假設。即不能認為血型與白血病病型有聯系。
表10 白血病人按病型和血型分組
回歸與相關 用來建立或明確兩種指標之間的關系的統計技術。前者可用於分析一個變量受另一變量影響的程度;後者則用於分析兩個對稱或“平等”的指標之間的關聯程度。
直線回歸是用簡單的直線方程尲=a+bx來擬合依變量y(尲表示它的估計值)受自變量x影響的情形。式中的a與b可以在有回歸功能鍵的計算器上直接得出,但需按說明書將成對的觀測數據(x,y)輸入。計算程序的原理在於使
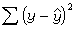 極小化。若自變量不止一個,則有尲=
b
0+
b
1
x
1+
b
2
x
2+…,稱為多元回歸,可用於預測、判別與指標的綜合等。一般的微電腦常有計算多元回歸系數
b
i等的程序。
極小化。若自變量不止一個,則有尲=
b
0+
b
1
x
1+
b
2
x
2+…,稱為多元回歸,可用於預測、判別與指標的綜合等。一般的微電腦常有計算多元回歸系數
b
i等的程序。
直線相關系數r=bSx/Sy(其中b為回歸系數,Sx、Sy分別為x與y的標準差),其絕對值反映兩個指標相關的程度。r的取值范圍是-1到+1。它也可以在計算器上直接得出。
概率單位分析法 主要用於處理生物對化學或物理刺激的反應曲線。是一種以劑量的對數為自變量,以反應率的概率單位為依變量,從而使S型曲線直線化而便於分析的一種方法,可用於測定藥物、毒物或物理因素對機體作用的強度和分析它們的聯合作用。
無分佈法 大多數統計分析方法都建立在“數據為正態分佈”這一基本假定之上,而許多生物學數據遠非正態分佈,采用無分佈法可以繞過這一困難。這類方法往往比較直觀,而且計算簡便。有時,一部分(或全部)觀測結果並不能直接用數據表示,隻能用反映大小或程度的等級或秩次表示。例如,觀測結果是“-”,“±”,“+”及“++”以上,排序後的等級便是1,2,3,4……。許多很有效的無分佈法就是基於數據或觀測結果的大小順序的。由於無分佈法通常並不涉及數據分佈的參數(如平均數),所以有時也稱為非參數方法。
生存分析 許多生物現象的動態觀察結果都比一次性的橫斷面觀察更能說明問題。例如:惡性腫瘤患者接受手術治療的效果,要看他們術後經過一段時間的生存率,或者有必要描繪出在不同條件下的生存率曲線(以時間為橫軸,生存率為縱軸),以便進行分析與比較;器官移植的效果,要看異體器官在體內正常工作和不被排斥的時間等。生存分析的用途是廣泛的。
多元分析 又稱多指標或多變量分析,是對多個觀測指標同時進行綜合性分析,所以比普通的一元統計分析更為全面、有效。這是40年代就已出現的一系列好方法。由於涉及較深的數學知識和很復雜的計算,妨礙瞭它們的普及,隨著計算機和統計軟件包的日益完善,預料多元分析不久將會成為生物科學研究的常規武器。多重回歸是指多個自變量和一個因變量的回歸;而多元回歸是指不止一個因變量的回歸。但二者常被混淆使用。它們可用於預測、指標的綜合或自變量的篩選。判別分析是利用形如多重回歸方程的判別函數來進行個體種類的判斷或診斷。聚類分析是將許多個體或指標按它們的相似程度來歸類。對個體進行聚類稱為Q型聚類;對指標進行聚類稱為R型聚類。Q型聚類和判別分析是數量分類學的兩種基本方法。趨勢面是以地理上的經、緯度為自變量的高次方程,可用於繪制研究對象在地理上的分佈密度的等高線圖,亦可用於預測。主成分分析的目的在於將許多彼此相關的指標變換成少數幾個彼此獨立的綜合指標,而且它們包含瞭原來那些指標的幾乎全部統計信息。因子分析的計算程序與主成分分析類似,但它不是研究指標的變換,而是分析個體間的內在聯系,此法為心理學傢所首創,也可用於研究復雜的疾病。
統計模型 幾乎所有的統計方法都有一個數學模型作為背景。除瞭上述方法之外,在生物科學研究中用處較大的還有:捉放捉模型,用於個體總數的估計;對數線性模型,用於多維列聯表(即按多個指標分組的計數資料)的分析;Logit模型,既可用來同時排除多個混雜因素的影響,又可用於處理定量的混雜變量與危險因子。如果所有指標都是定性的,Logit模型就成瞭對數線性模型的一個特例。
參考書目
楊紀珂等:《現代生物統計》,安徽教育出版社,合肥,1985。
湯旦林:《醫用統計基礎》,人民衛生出版社,北京,1989。
C.C.Li,Introduction to Experimental Statistics,McGraw-Hill Book Co.,New York,1964.
P.Armitage,Statistical Methods in Medical Research,Blackwell Seientific Publications,Oxford,1977.