可表示為分數
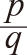 的數,其中
p、
q是整數,
q≠0。關於有理數的嚴格定義,見
數。有理數可進行四則運算:對於
的數,其中
p、
q是整數,
q≠0。關於有理數的嚴格定義,見
數。有理數可進行四則運算:對於
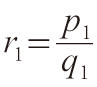 ,
,
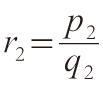 有
有
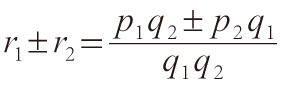 ;
;
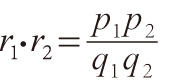 ;
;
 (假定
r
2≠0即
p
2≠0)。有理數集關於加法與乘法構成一個域。有理數之間還有序關系≤,滿足通常的有關性質。
(假定
r
2≠0即
p
2≠0)。有理數集關於加法與乘法構成一個域。有理數之間還有序關系≤,滿足通常的有關性質。
正分數出現很早。埃及賴因德古本(約前1650)中就有很多涉及分數的題。現存的巴比倫泥板文書(前2000年前後和前600~前300)中也有楔形符號表示的分數。中國至遲在春秋時期(前770~前476)已有關於分數的記載,到戰國時期(前475~前221)分數運算已很普遍。
“有理數”以及與之相對的“無理數”這兩個詞起源於希臘。畢達哥拉斯學派稱能表示為自然數之比的兩個量為可公度的,否則稱為不可公度的。古希臘人用ρητοζ (ratos,可比)或λογοζ(logos,可表達)表前者,用αρρητοζ(arratos,不可比),αλογοζ(alogos,不可表達)表後者。ratos轉為拉丁文ratio,除“比”外還有“理由”之意。6世紀羅馬人卡西奧多拉斯首先在現代意義下使用“有理數”、“無理數”這兩個詞。阿拉伯數學傢花拉子米把alogos意譯為阿文“聽不見”,後轉譯為拉丁文surdus,英文為surd(不盡根,無道理)。
有理數的非整數部分也可以用十進制小數表示,如1/2=0.500 0,2/3=0.666 6…,2/7=0.285 714 285 714…與有理數對應的小數都是有限小數或無限循環小數。有理數集合是可數的,也是稠密的(即任意兩個有理數之間總存在著有理數)。可以證明有理數與自然數之間可以建立一個一一對應,因此有理數集是可數集,全體有理數組成的集合的基數等於自然數的基數。