基於狀態空間描述（見狀態空間法）對混有雜訊的信號進行濾波的方法，簡稱卡爾曼濾波。這種方法是R.E.卡爾曼和R.S.佈希於1960和1961年提出的。卡爾曼濾波是一種切實可行和便於應用的濾波方法，其計算過程通常需要在電腦上實現。實現卡爾曼濾波的裝置或軟體稱為卡爾曼濾波器。
特點 從混有雜訊（幹擾）的信號中濾除雜訊、提取有用信號是濾波的基本目的。在卡爾曼濾波出現以前，已經建立瞭採用用最小二乘法處理觀測數據和采用維納濾波方法處理平穩隨機過程的濾波理論。但這些濾波方法或因功能不夠，或因條件要求苛刻，而不便於實用。卡爾曼濾波是在克服以往濾波方法的局限性的基礎上提出來的，是濾波方法的重大演進。卡爾曼濾波比維納濾波有以下優點：①在卡爾曼濾波中采用物理意義較為直觀的時間域語言，而在維納濾波中則采用物理意義較為間接的頻率域語言。②卡爾曼濾波僅需要有限時間內的觀測數據，而維納濾波則需要用過去的半無限時間內的全部觀測數據。③卡爾曼濾波可使用比較簡單的遞推算法，而維納濾波則需要求解一個積分方程。④卡爾曼濾波可以推廣到非平穩隨機過程的情況，而維納濾波隻適用於平穩隨機過程。⑤卡爾曼濾波所需數據存儲量較小，便於用計算機進行實時處理，而維納濾波的計算復雜，步驟冗長，不便於實時處理。在相同條件下，卡爾曼濾波能得出與維納濾波相同的結果。在實用上，卡爾曼濾波比維納濾波功能強，用途廣。卡爾曼濾波已在航天技術、通信工程、工業控制等領域中得到比較廣泛的應用。卡爾曼濾波的局限性表現在隻能用於線性的信號過程，即狀態方程和觀測方程都是線性的隨機系統，而且噪聲必須服從高斯分佈。雖然不少實際問題都可滿足這些限制條件，但當實際系統的非線性特性稍強或者噪聲特性偏離高斯分佈較大時，卡爾曼濾波就不能給出符合實際的結果。
原理 線性離散隨機系統用如下離散時間的動態方程和觀測方程描述：
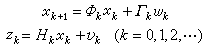
式中x和z分別為系統的狀態向量和觀測向量，ω和v均為零均值的高斯白噪聲,Ф、Γ 和H為系統矩陣,下標k表示離散時間。假定初態x0的均值Ex0＝x0(E表示均值)和方差陣varx0＝P0（var表示方差）均為已知,且最小方差意義下xk的最優線性估值X̂k已經求得,則有X̂k+1|k＝ФkX̂k。其中X̂k+1|k表示X̂k+1在xk的最優估值為X̂k的條件下的一步最優預測估值。相應的誤差方差陣則為
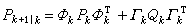(上標T表示矩陣轉置),其中
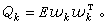一步最優預測估值X̂
k+1|k需要經觀測值
zk
+1的修正後才能得到
xk
+1的最優估值X̂
k
+1，即
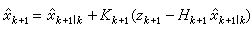
這個方程右端的第二項表示校正項，其中括號內的項稱為新息。Kk+1 稱為增益陣。因此卡爾曼濾波方法可直觀表述為在一步最優預測估值的基礎上增加新息校正。新息是由第k＋1步觀測決定的，其中包含由噪聲引起的觀測誤差。增益矩陣 Kk+1對它有調節作用，當噪聲很大時Kk+1的元會自動地取較小的值,反之則取較大的值。卡爾曼濾波的四個遞推方程是：
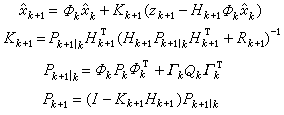
式中Rk＝Evkv
，
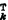I表示單位矩陣,上標-1表示矩陣求逆，
Pk＝var(
xk-X̂
k)為濾波誤差方差陣。這四個方程所表示的遞推算法就是卡爾曼濾波，從初始值出發由此可遞推地算出任一時刻
k的最優估值X̂
k。對於連續時間情況也有類似的方程組，但差分方程將為微分方程所代替。在卡爾曼濾波中,當噪聲{
wk}和{
vk}為白噪聲時，X̂
k是
xk的所有線性估計中的最小方差估計。而當{
wk}和{
vk}為高斯白噪聲時，X̂
k是
xk的所有估計中的最小方差估計。由於這個緣故，卡爾曼濾波也常被稱為最優濾波。
參考書目
A.P.塞奇、I.L.梅爾薩著，田承駿、唐策善等譯：《估計理論及其在通訊與控制中的應用》，科學出版社，北京，1978。(A.P.Sage and J.L.Melsa，Estimation Theory with Applications to Communications and Control, McGraw-Hill, New York,1971.)
中國科學院數學研究所概率組編：《離散時間系統濾波的數學方法》，國防工業出版社，北京，1975。