拉格朗日方程

　　完整系統（見約束）用廣義座標表示的動力學普遍方程。它是J.L.拉格朗日在1788年所得到的。其典型表示式為

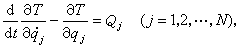(1)

式中T是系統的動能，它必須用N個廣義座標>q_j(j=1，2，…，N)和N個廣義速度

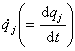來表示； Q _j是對應於廣義坐標 q _j的 廣義力。

　　對於保守系統還存在著勢函數V(q₁，q₂，…，q_N)，因為有

和 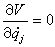，所以令 L= T- V後，式(1)即為

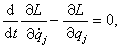
式中

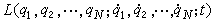稱為拉格朗日函數或稱為動勢。 L的量綱同能量，即 L ² MT ^-2。

　　從式 (2)中可以求出下面兩種特殊情況下的一次積分：

　　① 廣義動量積分。如果在動勢L的表示式中不包含屬於系統的廣義坐標q_k，這種坐標稱為循環坐標或稱可遺坐標。根據這個定義，有

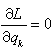，於是由拉格朗日方程 (2)則有 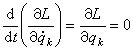。積分上式得 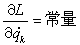。=常量。 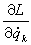稱為對應於廣義坐標 q_k的 廣義動量，用 p_k表示，是常量，於是對應於循環坐標的廣義動量是守恒的。

　　② 廣義能量積分。亦稱雅可比積分。當一個完整系統的動勢L不顯含時間t時，即可求得雅可比積分

T₂-T₀+V=H常量， (3)

式中T₂表示動能T用廣義速度

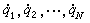和廣義坐標表示時，對於 T中含廣義速度的二次齊次式的部分； T ₀表示 T中不含廣義速度的部分； V是勢函數。

　　當一個完整系統的約束方程都不顯含時間t時，這種系統稱為自然系統。對這樣的系統，動能是廣義速度的二次齊次式，即T=T₂。這樣，雅可比積分化為能量積分：T+V=H。所以稱式(3)為廣義能量積分。

　　拉格朗日方程有下列特點：①拉格朗日方程是用廣義坐標表示的，對於實際力學問題可根據問題的特點選取適宜的廣義坐標來建立動力學方程，從而便於求解。②對於具有n個質點和h個有限約束的完整系統，拉格朗日方程有N=3n-h個二階微分方程。但是用直角坐標表示的牛頓方程有3n個二階微分方程，連h個有限約束方程，共有3n+h個方程。二者比較，拉格朗日方程較便於求解。③應用拉格朗日方程可導出力學中的變分原理──哈密頓原理，和另一組重要的運動微分方程──哈密頓正則方程。