表示線性時不變系統輸入量(或激勵)與輸出量（或回應）關係的一種函數。

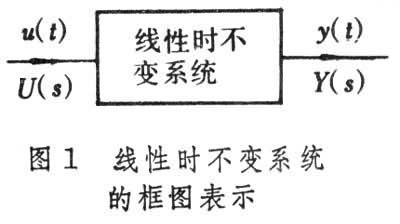
　　對於一個單輸入、單輸出連續的線性時不變系統（圖1），，設輸入為u(t)，輸出為y(t)，它們的拉普拉斯變換分別為

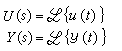
　　在零狀態的情況下，輸出Y(s)與輸入U(s)之比，是一個僅依賴於系統結構和系統參數的復變量s的函數，記作H(s)，稱為此系統的傳遞函數

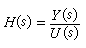
一個集總的線性時不變系統，其輸入-輸出關系由一常系數線性微分方程表征，由之容易求出其傳遞函數。設系統的微分方程是

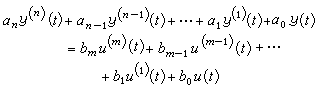相應的傳遞函數即是

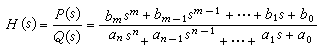
　　集總的線性時不變系統的傳遞函數是s的有理函數，即兩個s的多項式之比。其中的系數均為實數。對於分佈參數系統，傳遞函數由相應電路的偏微分方程確定，它們往往是復雜的。

　　描寫電路的方程，還可以有多種形式的。例如在電路中可以用節點電壓法或回路電流法寫電路方程，求得所需的傳遞函數。

　　圖2中兩個電路的傳遞函數如下。

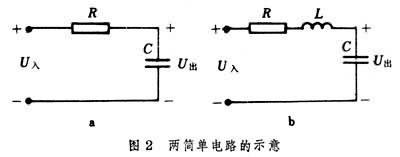圖2a的電路的傳遞函數是

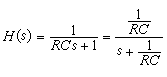
圖2b的則是

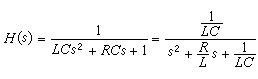
　　已知一個系統的傳遞函數，給定其輸入，就可由拉普拉斯反變換求得輸出

　　復雜系統的傳遞函數　一個復雜的系統常可劃分為若幹個單向的環節或部分的組合。所謂單向的環節，是指信號隻能夠向一個方向即由輸入到輸出的方向傳遞的環節。在這種情況下，系統的傳遞函數可以簡單地用各環節的傳遞函數的乘積表示。

　　常用方框圖表示一個復雜系統的信號的傳遞方式。一個方框的輸入-輸出用其傳遞函數表示(圖3a)，

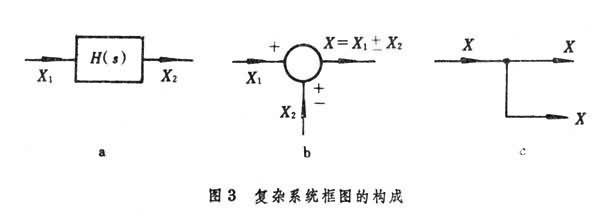根據系統的方程式將各個方框用圖3b的比較點和圖3c的分支點聯接起來，就得到系統的框圖。根據系統的框圖，由各方框的傳遞函數及比較點、分支點處的輸入-輸出關系，即可推出整個系統的傳遞函數。

　　傳遞函數與頻率特性　一個系統的傳遞函數僅決定於系統的結構與其中的參數，而與輸入(激勵)無關。其實，可以更簡便將傳遞函數理解為施加est[t∈(-∞，∞)]形式的激勵時輸出與輸入之比。此比值是復頻率s的函數。如取s＝jω，則

H(s)

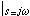= H( j ω)

即為系統在角頻率為 ω的正弦穩態下的輸出-輸入之比，稱為系統的頻率特性。將它記作

H(jω)=|H(jω)|

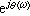的形式。其中| H( j ω)|稱為此傳遞函數的幅頻特性，它表示輸出與輸入的振幅之比； θ( ω) 稱為此傳遞函數的相（角）頻特性，它表示輸出輸入的相位差。它們均隨角頻率 ω的變化而變化，所以都是 ω的函數。除瞭根據系統的結構、參數由上式那樣的方程計算系統的傳遞函數，求得其頻率特性以外，還可以用實驗測量輸入、輸出的方法求得系統的頻率特性。

　　對一系統的特性的研究可以代之以對其傳遞函數或頻率特性的研究。電路、線性系統的分析、設計在很大程度上就轉化為相應的傳遞函數的分析、設計。因此，傳遞函數成為研究線性時不變系統廣泛使用的工具。

　　傳遞函數還可推廣用以表示多變量系統（多輸入、多輸出的系統）。例如一個2輸入2輸出系統的H(s)便是一個2×2的矩陣，它的每一元素相當於在某種條件下由此多變量系統形成的單變量系統的傳遞函數。

　　離散時間系統也常用其傳遞函數來描述和分析。

　　傳遞函數的零點和極點　一系統的傳遞函數決定它的輸入輸出關系，它的拉普拉斯反變換即是系統的沖激響應。可見它的性質對系統的輸出起著重要的作用。而傳遞函數作為復變量(復頻率)s的函數的特性可以由它的零點和極點的分佈來表征。

　　集總參數電路的傳遞函數的一般形式是實系數的有理函數，將此式寫作以下形式

式中 z i、 p j可以是復數或實數值。使分子多項式 P( s)為零的各復頻率 z i值，稱為傳遞函數的零點；使分母多項式 Q( s)為零的各復頻率 p j值，稱為傳遞函數的極點，又稱自然頻率。它們決定瞭系統輸出中的自由振蕩的模式。這隻要將輸出的拉普拉斯變換式作部分分式展開，即得

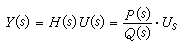假定 Q( s)=0無重根， U( s)的極點是單重的

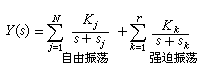
式中N是Q(s)=0的零點數，r是激勵U(s)的極點數。這裡假定H(s)、U(s)的零點極點沒有相同的（有與極點相同的零點，表示Y(s)的分子、分母中有公因子，可以先將其消除）。於是輸出y(t)便有以下形式

由此可見，- s j是對應於輸出中自由振蕩分量 e 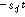的自然頻率，而- s K則是輸出中的強迫振蕩分量 e 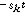的復頻率。零點決定輸出中每一分量的大小，因為它們影響 K j、 K r諸系數的值。

　　傳遞函數零點極點的分佈與系統的輸出性狀的關系可以歸納如圖4所示。

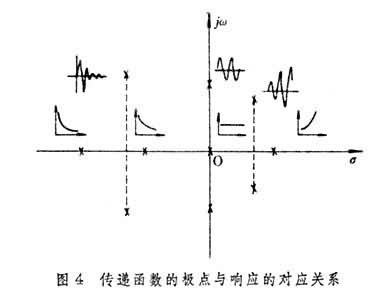由於決定極點位置的方程式的各系數均為實數，所以它若有復數根，則它必以共軛對出現，即若 S j為其復數根， S j的共軛 s j亦必為其根。假定所有的極點都是單重的。這樣，圖4中的每一對實部為負的共軛復根對應於輸出中的衰減振蕩分量，根的實部決定衰減的快慢，根的虛部確定振蕩的角頻率；在虛軸上的一對共軛虛根對應於輸出中的不衰減的正弦振蕩；在原點的極點對應於輸出中的恒定分量；在負實軸上的極點對應於輸出中的指數衰減分量；在右半面上的極點對應於指數增長（絕對值）的分量。

　　傳遞函數有極點在閉右半s平面的系統是不穩定的，因為其中的自由振蕩隨著時間t的增加而無限增長。穩定的系統的傳遞函數的極點均限制在開左半s平面。根據極點零點在s平面上的分佈，可以對系統的多方面的性狀，如穩定性、頻率特性、動態性質等進行分析研究。