由於地殼中巖層重迭,並受長期的地質構造作用,巖體中各點的應力不同,可認為是空間和時間的函數。地殼中巖體應力分佈狀態稱原巖應力場。巖體應力是分析判斷巖土工程穩定性和採礦工程結構的基礎資料。影響巖體應力形成的因素為:巖石的物理力學性質、地質構造及活動過程、地形條件、地下水、瓦斯以及人類生產活動等。巖體應力場主要由自重應力場、構造應力場以及因採掘工作引起的次生應力場構成。
自重應力場 金尼克(Α.Н.Динниκ)於1925年根據均質各向同性線彈性體假設,提出原巖應力計算公式:垂直方向主應力等於單位底面積上的巖土體自重,即σz=αZ,式中α為上覆巖層的平均容重,Z為深度。兩個水平方向主應力σx=σy=λ σz,側應力系數λ=μ/(1-μ),式中μ為泊松比,一般巖土體的μ≈0.2~0.3,λ≈0.25。1912年,海姆(Heim)從巖土體有流變性出發,認為原巖體大都處於各向等壓即靜水壓力狀態,也可認為距地表深度較大時,因巖石呈塑性狀態μ=0.5,λ=1巖體也會處於靜水壓力狀態:σx=σy=σz。
構造應力場 使初始呈水平沉積地殼形成山巒重迭的構造體系和構造型式的應力場。20世紀30年代中國地質學傢李四光指出,地球自轉速度變化,會在地殼中產生東西方向和南北方向作用的水平力。水平方向兩個應力的數值和(σx+σy)遠大於垂直應力的數值σz。50年代以後,隨應力測量技術發展,美、蘇、加、澳、中等國根據實測資料揭示,大多數情況下原巖水平應力比垂直方向主應力大1~3倍或更大;兩水平軸向的主應力也並不相同,比值為0.3~0.8;垂直方向應力通常等於自重應力,有時為自重應力的1.5~3倍。原巖主應力方向,常稍偏離垂直和水平方向,這主要是受地質構造運動殘餘應力場的影響。
次生應力場 巷道開掘,破壞原巖體的應力平衡,應力重新分佈後形成的應力場見圖(圖中符號所代表的量見自重應力場)。沿巷道斷面水平軸線方向,應力重分佈的特點見圖左部:剪應力增加的幅度,靠近巷道周邊最大,越遠越小。應力變化的數值,隨巖性、深度、巷道斷面形狀和尺寸、開采條件和時間等因素而定。在巷道圍巖的某些局部,由於原巖垂直應力與水平應力的比值、巷道斷面形狀、尺寸及巖體產狀的不同,可能出現對巷道穩定極為不利的拉應力。應力重新分佈時,巷道圍巖釋放潛能,迫使圍巖向巷道空間移動。此後,如最大應力不超過巖石強度條件,圍巖可自穩;否則,在圍巖中將出現大小不等的破裂松動區,見圖1右部。在松軟巖石中,破裂過程的擴容為原體積的0.05~0.40,所造成位移的總量達10~50cm以上。
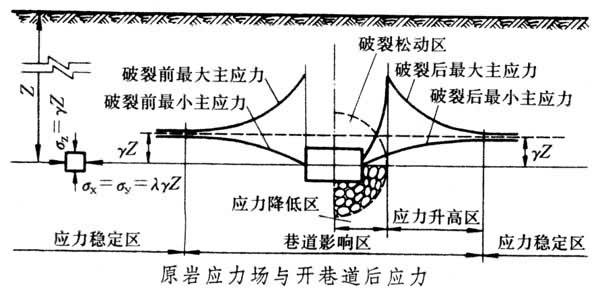
巖體應力、應變的特征之一,是達到破裂極限後的應力急劇降低,巷道圍巖破裂區內的應力降為殘餘應力,形成應力降低區。由於該區內的部分巖體喪失承載能力,致使上覆地層重力繞過該區轉嫁到鄰近區域,與原有應力疊加,形成應力升高區。應力降低區與升高區,合稱巷道影響區。其范圍約為巷道斷面最大尺寸的3~5倍。以應力升高值剛超過原巖應力5%的地方,作為巷道影響區的邊界。開巷後應力升高區的應力與原巖應力的比值K,稱應力集中系數。方形或矩形斷面巷道的直角拐點,理論上的K值為無限大。由於施工原因,該點處實際總是略呈圓弧,K值降為5~7,但仍比圓形、橢圓形斷面的應力集中系數為大。
在受到采場圍巖應力場的影響時,巷道圍巖應力場會再次重新分佈,導致應力疊加。這種影響稱為采動影響。采準巷道經受采動影響後,它的應力場將更為復雜。
原巖應力主要用“應力解除”和“水力壓裂”等方法實測確定。巷道圍巖的應力場可用彈塑性力學、有限元法、邊界元法、流變學等理論和數值方法,光彈、全息光彈、相似材料模型、離心模型模擬方法,以及與上述實測方法等結合研究。
參考書目
L.Obert &W.L.Duvall,Rock Mechanics and the Design ofStructures in Rock,John Wiley &Sons,New York,1967.