斷裂學科的一個分支，從構件記憶體在著宏觀裂紋出發，應用線彈性力學和彈塑性力學方法進行分析和實驗，從而對含裂紋的構件的安全性和壽命給出定量的或半定量的估算，提供構件的設計、驗收、選材以及斷裂韌性測定的理論基礎。20世紀20年代，格裏菲思(A.A.Griffith)試圖解釋玻璃的理論斷裂強度和實測值之間的巨大分歧時，提出瞭由於固體記憶體在著裂紋，造成大的應力集中，使局部的裂紋擴展而造成斷裂。他進一步從能量觀點提出斷裂判據：如果裂紋擴展所釋放的彈性應變能足以提供裂紋紋擴展所需的表面能時，則裂紋擴展。但由於其數學-力學推導中沒有考慮在裂紋前端的塑性變形功，所以結論僅能用於玻璃一類的脆性材料。以後歐文(G.R.Irwin)(1948)和奧羅萬(E.Orowan)(1947)分別註意到，對於延性材料，局部的范性形變所作的功應該加入裂縫擴展的能量公式中；在裂縫擴展過程中，如果不供給足夠的能量，則裂縫的擴展被抑止。1957年歐文運用韋斯特加德(Westergaard)應力函數，求出中心穿透裂紋板材雙向受拉時的彈性力學解，這是運用力學方法認識復雜的斷裂過程並走向工程實用的重要的一步(見形變和斷裂)。根據對裂紋附近材料所假定的狀態不同，分為線彈性斷裂力學和彈塑性斷裂力學，前者較為成熟。
線彈性斷裂力學 分析裂紋附近的應力狀態的出發點是：裂紋前端的塑性區足夠小，因此其周圍材料的應力（σ）和應變（ε）的關系仍是線性的。由此來研究裂紋前端的應力場、應變場以及同裂紋擴展有關的能量關系，提出在這種條件下的裂紋擴展的判據。
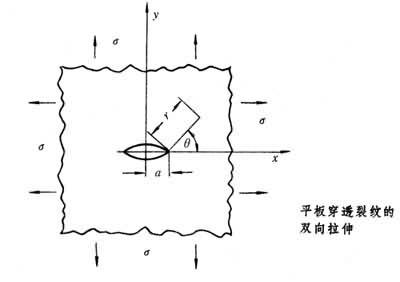
構件中存在著裂紋並受到外載荷時，裂紋和載荷通常有三種組合形態：張開型（Ⅰ型）、滑開型(Ⅱ型)和撕開型（Ⅲ型），其中以Ⅰ型最危險，因此，即使是復合型的組合，也可以按照Ⅰ型來建立失穩判據。歐文求出瞭如附圖所示的平板穿透裂紋雙向受拉時的應力分佈的解為：
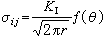(1)
式中
，
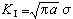K
I叫作應力場強度因子；
a為裂紋的長軸長度的一半；(
r，
θ)為所求點的極坐標；
f(
θ)為角
θ的函數。
由上式再列入關於塑性區的修正，就可以求出Ⅰ型裂紋擴展時的能量釋放率GI，有實用意義的情況是
平面應力時：
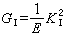(2)
平面應變時：
(3)
式中E為材料的彈性模量；υ為材料的泊松比。
也可以研究更為普遍的、不限定裂紋為中心穿透的裂紋的情況，此時
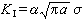(4)
式中
α為與裂紋幾何形狀和加載方式有關的無量綱系數，中心穿透裂紋雙向受拉時，
α＝1；
a為與斷裂過程有關的裂紋特征尺寸。
由此可以得到斷裂判據：當KI達到某個臨界值KIc時，裂紋迅速擴展而致斷裂，此時的應力記為σF，裂紋長度記為ac，則
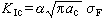(4a)
由此式可以測定各種材料的
K
Ic，並求出適用於工程設計的斷裂判據。
K
Ic叫作平面應變時的材料斷裂韌度，或簡稱為斷裂韌度。但是應該指出，由於被其分析的基礎決定，所得的結果隻適用於在低應力下發生脆性斷裂時的情況，一般為：
σF≤0.6σs(5)
式中 σ F為材料的斷裂應力， σ s為屈服強度。彈塑性斷裂力學 當裂紋前端的塑性區的相對尺寸較大時，線彈性關系不再適用，也就是不能再運用KI≥KIc作為斷裂判據。此時，要用彈塑性力學處理裂紋體的斷裂問題。在實驗的基礎上提出新的斷裂韌性參量，得到新的斷裂判據。目前比較成熟的判據有：
① 應變判據 認為裂紋的頂端張開位移（crack opening displacement或簡寫為COD）達到臨界值(δc)時，裂紋失穩擴展，材料斷裂。對於薄板雙向受拉時的Ⅰ型穿透裂紋，可以導出以下關系：
(6)
展開：
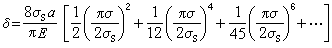(7)
對於低應力〔例如(5)式〕，可近似地隻取無窮級數中第一項，則：
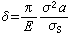(8)
將(4)式代入，並考慮臨界條件，則得到：
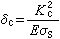(9)
式中
K
c為平面應力時的斷裂韌度。
② 能量釋放率判據 當能量釋放率GI達到臨界值GIc時，斷裂發生。在彈塑性條件下，確定瞭GI等值於某個沿圍繞裂紋的團合回路的積分JI。可以證明JI值與積分路徑無關，因而可把在特定條件下的實驗測定臨界值JIc用於彈塑性條件下的斷裂判據。在線彈性條件下：
JIc=GIc(10)
斷裂力學討論和處理瞭材料受力時裂紋的擴展條件和斷裂判據，也可以用來分析在其他條件下，如疲勞、應力腐蝕（見應力腐蝕斷裂和氫脆）等裂紋的形成和擴展；同時也就能夠用於研究在各種條件下防止斷裂的措施以及提高材料的斷裂韌性的途徑。
參考書目
肖紀美：《金屬的韌性與韌化》，上海科學技術出版社，上海，1980。