經典力學的一個分支。它用幾何方法描述物體的運動，而不考慮力和品質等因素。至於物體的運動和力的關係則是動力學的研究課題。要描述物體的運動必須確定一個參照系，因此，單純從運動學的觀點看，對任何運動的描述都是相對的。這裏，運動的相對性是指經典力學範疇內的，即在不同的參照系中時間和空間的量度相同，和參照系的運動無關。物體的速度接近光速時，時間和空間的量度就同參照系有關瞭（見狹義相對論）。
在運動學中主要研究點和剛體的運動規律。點點是指沒有大小和質量、在空間占據一定位置的幾何點。剛體是沒有質量、不變形、但有一定形狀、占據空間一定位置的形體。運動學包括點的運動學和剛體運動學兩部分。
歷史概述 運動學在發展的初期，從屬於動力學，隨著動力學而發展。古代，人們通過對地面物體和天體運動的觀察，逐漸形成瞭物體在空間中位置的變化和時間的概念。中國戰國時期在《墨經》中已有關於運動和時間先後的描述。亞裡士多德在《物理學》中討論瞭落體運動和圓運動，已有瞭速度的概念。伽利略發現瞭等加速直線運動中距離與時間二次方成正比的規律，建立瞭加速度的概念。在對射彈體運動的研究中，他得出拋物線軌跡，並建立瞭運動（或速度）合成的平行四邊形法則，伽利略為點的運動學奠定瞭基礎。在此基礎上，C.惠更斯在對擺的運動和I.牛頓在對天體運動的研究中各自獨立地提出瞭離心力的概念，從而發現瞭向心加速度同速度的二次方成正比、同半徑成反比的規律。
18世紀後期，由於天文學、造船業和機械業的發展和需要，L.歐拉用幾何方法系統地研究瞭剛體的定軸轉動和剛體的定點運動問題，提出瞭後人用他的姓氏命名的歐拉角的概念，建立瞭歐拉運動學方程和剛體有限轉動位移定理，由此得到剛體瞬時轉動軸和瞬時角速度矢量的概念，深刻地揭示瞭這種復雜運動形式的基本運動特征。歐拉可稱為剛體運動學的奠基人。J.L.拉格朗日和W.R.哈密頓分別引入瞭廣義坐標、廣義速度（見拉格朗日方程）和廣義動量，為在多維位形空間和相空間中用幾何方法描述多自由度質點系統的運動開辟瞭新的途徑，促進瞭分析動力學的發展。
19世紀末以來，適應不同生產需要、完成不同動作的各種機器相繼出現並廣泛使用，於是，機構學應運而生。機構學的任務是分析機構的運動規律，根據需要實現的運動設計新的機構和進行機構的綜合。現代儀器和自動化技術的發展又促進機構學的進一步發展，提出瞭各種平面和空間機構運動分析和綜合的問題，作為機構學的理論基礎，運動學已逐漸脫離動力學而成為經典力學中一個獨立的分支。
點的運動學 描述點在空間的位置隨時間變化的規律。點在空間所經過的路線稱為軌跡，按軌跡形狀可分為:點的直線運動、點的平面曲線運動（如圓周運動，橢圓運動和拋物線運動等）和空間曲線運動（如空間螺旋線運動）。空間曲線運動是最一般的情況。點在參照系中的位置用點對於某固定點的矢徑r 表示，點的運動規律用矢徑的時間函數r＝r(t)表示。點的速度和加速度分別用矢徑對時間的一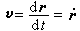階導數
和二階導數
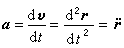表示。通常用如下幾種坐標系來表示點的運動。
直角坐標系 點的位置用直角坐標x、y、z表示。點的運動規律表示為
r＝x(t)i +y(t)j +z(t)k，
式中i、j、k為沿坐標軸的三個單位矢量。
x＝x(t)， y＝y(t)， z＝z(t)
是點的直角坐標運動方程，也可看成是以t為參變量的軌跡方程。點的速度和加速度可分別表示為
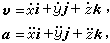
用在 x、y、z上加一個或兩個圓點表示對時間的一階或二階導數。
自然軸系 如果點的軌跡已知(圖1)， 點沿軌跡運動的規律用軌跡上的定點O到M點的弧長（弧坐標）s(t)表示。點的速度和加速度可分別表示為
，
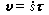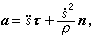
式中ρ為軌跡的曲率半徑；τ、n和b(圖1)是分別沿切線、主法線和次法線的三個單位矢量；b＝τ×n構成自然軸系。
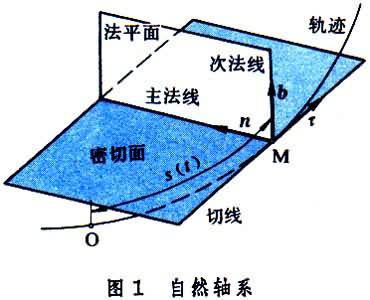
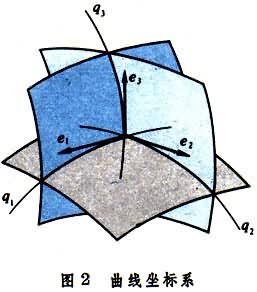
曲線坐標系 可用三個獨立變量 q1、q2、q3表示點在空間的位置(圖2)。如直角坐標x、y、z和曲線坐標q1、q2、q3之間有一一對應關系，則點的矢徑可表示為曲線坐標的矢量函數r=r(q1，q2，q3)。如建立一正交曲線坐標系，e1、e2、e3為沿坐標曲線的切線的三個單位正交矢量，
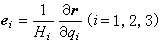。點的速度和加速度可分別表示為
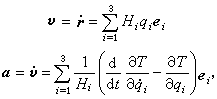
式中
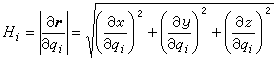，即拉梅系數；
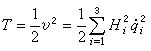。直角坐標、柱坐標和球坐標都是正交曲線坐標的特例。
剛體運動學 研究剛體的各種運動規律。按剛體運動形式可分為以下幾種運動。
平動(平移) 運動中剛體上任一直線保持平行；剛體的運動可歸結為剛體上任一點的運動。
定軸轉動 剛體上一軸線固定不動，剛體的運動方程為θ＝θ(t)。剛體的角速度和角加速度分別為
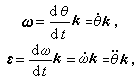
式中k為沿轉動軸的單位矢量。
平面運動 剛體上任一點在運動中始終和一固定平面距離不變，剛體的運動方程為
rO＝rO(t)，θ＝θ(t)，
式中rO為剛體上某一點 O(基點)對參照系中固定點的矢徑，如剛體上任一點對基點的矢徑為r′，則此點的速度和加速度分別為
v＝vO+ω×r′，α＝αO+ α×r′+ω×(ω×r′)，
式中vO和αO分別為基點 O的速度和加速度；ω和α分別為剛體轉動的角速度和角加速度。剛體的瞬時運動可歸結為繞瞬時轉動中心的轉動（見剛體的平面運動）。
定點運動 剛體上一點固定不動，剛體的運動方程可用歐拉角表示為
φ＝φ(t)，θ＝θ(t)，ψ＝ψ(t)。
如剛體上任一點到定點的矢徑為r，則此點的速度和加速度分別為
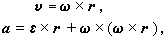
式中ω和α為剛體的瞬時角速度和角加速度矢量。剛體的瞬時運動可歸結為繞瞬時轉動軸的轉動。
空間一般運動 這是自由剛體運動的最一般形式。可把剛體的運動分解為隨基點O的平動和繞基點O作定點運動。剛體的運動方程為
rO＝rO(t)，φ＝φ(t)，θ＝θ(t)，ψ＝ψ(t)。
如剛體上任一點對基點的矢徑為r′，則此點的速度和加速度分別為
v＝vO+ω×r′，
α＝αO+α×r′+ω×(ω×r′)，
式中vO和αO分別為基點的速度和加速度；ω和α分別為剛體的瞬時角速度和角加速度矢量。剛體的瞬時運動可歸結為繞瞬時螺旋軸作螺旋運動。
參考書目
A. Wolf， A History of Science Technology and Philosophy in the 16th and 17th Centuries，George Allen & Unwin， London，1935.
R. Dugas， A History of Mechanics，Routledge & Kegan Paul， London，1957.