由地震震源向四處傳播的振動。地震學的主要內容之一就是研究地震波所帶來的資訊。地震波是一種機械運動的傳佈，產生於地球介質的彈性。它的性質和聲波很相近，因此也叫做地聲波，不過普通的聲波是在氣體中傳播的，而地震波是在地球介質中傳播的，所以要複雜得多。在計算上地震波和光波有些相似之處。波動光學在短波的情況下可以過渡到幾何光學，從而簡化瞭計算。同樣地，在一定條件下地震波的概念可以用地震射線來代替而形成瞭幾何地震學。不過光波隻是橫波，地震波卻縱、橫兩部分都有，在具體的的計算中，地震波要復雜得多。

　　地球介質和彈性波　地震波既然是地下傳播的震動，它的特征必然與巖石的物理性質有關系，特別是巖石的彈性。計算時，一般都假定巖石是一種完全彈性體。這看來似乎與事實不完全符合，因為不但地表的土壤與彈性體相差很遠，就是有些巖石（如頁巖）也不是彈性體。不過地震波所經過的途徑主要在地下深處，表土的影響不大。地震波的傳播速度很大，它所施加於巖石的應力是短暫的，能量的消失也是很小的。這樣，巖石的完全彈性便是一個可以允許的幾近假設。

　　巖石是由結晶的顆粒組成的，晶軸的取向一般是雜亂無章的。地震波長的尺度比晶粒的尺度要大得多，所以巖石晶粒的方向性和細微的物性差別對地震波的影響不大。在一般的地震波計算中，地球介質可以做為各向同性的完全彈性體來對待。不過應指出，在特殊的地區和精細的觀測中，地震波的傳播有時也表現出各向異性和能量消失。這些現象在某些問題中恰恰是需要研究的問題。

　　彈性常數　根據經典的彈性力學理論，一個各向同性的完全彈性體隻有兩個獨立的彈性常數。常用的彈性常數有以下幾個：楊氏模量E，剛性模量n，容積模量K，泊松比v和拉梅常數λ、μ。這些都是正值，它們之間存在以下的關系：

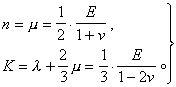　 (1)

所以實際上隻有兩個常數是彼此獨立的。計算時，任選兩個原則上都一樣（當然不能取n、μ）。

　　縱波和橫波　地震波到達之處，介質就產生形變。由力學定律知道，任何小的形變都可以分解為兩部分：一部分表示脹縮，即變體積而不變形狀；另一部分表示畸變，即變形狀而不變體積。形變傳播時，兩部分的傳播速度不同。在震源附近，兩部分還未分開，所以波經過處的形變是復雜的。在較遠的地方，波陣面就分成兩個。脹縮波傳播較快，波陣面上的質點位移和傳播方向一致，所以叫做縱波，一般用字母P表示。較慢的叫畸變波，質點位移和傳播方向垂直，所以叫做橫波，一般用字母S表示。在均勻的介質中，波陣面在震源附近是曲面，但在相當距離後就趨近於平面。為簡單起見，現隻討論平面波。在直角坐標系(x，y，z)中，取x平行於傳播方向，則(y，z)面與波陣面平行。令質點位移的3個分量各為ξ、η、ζ，則由彈性力學得到以下3個運動方程：

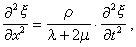　　　　　(2)

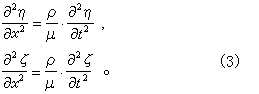
式中ρ是介質的密度，λ 、μ是拉梅常數，t 是時間。3個方程都具有波動方程的形式。方程(2)表示縱波，因為ξ與傳播方向x一致；方程(3)表示橫波，因為η和ζ都與x垂直。由(2)可見，縱波的傳播速度vP是

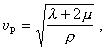　 　　　 　(4)

由(3)可見，橫波的傳播速度vS是

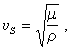　　　 　(5)

因ρ、λ 、μ全是正數，所以

vp>vs，

即是說，在介質中任一點的縱波速度恒大於同一點的橫波速度。若介質是一泊松固體，即是說若λ =μ或v =1/4，則

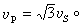由上式可見 ，地震波速度決定於介質的彈性與密度之比，在地球內部，巖石的彈性和密度都是隨深度而增加的，不過彈性增加得更快些，所以地震波的速度一般是隨深度而增加的，隻有在個別地區或個別深度情況下除外。

　　體波和面波　在沒有邊界的無限介質中，隻能有P波和S波存在，它們可以在三維空間中向任何方向傳播，所以叫做體波。但地球是有限的，有邊界的。在界面附近，還可能有另一種波動存在，它們隻能沿著界面傳播，在垂直於界面的方向並不傳播，這種波叫做面波。面波有多種，最重要的叫做瑞利波和洛夫波。瑞利波存在於地球表面之下，是1885年英國物理學傢瑞利(J.W.S.Rayleigh)首先在理論上導出，以後在地震記錄中得到證實。這種波的振幅在地面最大，隨著深度而指數縮減。它有一定的傳播速度vR，比橫波速度vs略小一些。當波向前傳播時，介質質點的運動軌跡是向後倒轉的橢圓。這樣的運動不是單純的脹縮或畸變。瑞利波不是單純的P或S，而是兩種成分都有。洛夫波是1911年英國力學傢洛夫(A.E.H.Love) 首先提出的。這種波發生時，介質至少要有兩層，上層中的vs要小於下層中的vs。面波存在於分界面之下，傳播速度介於上下層兩個橫波速度之間。洛夫波是橫波，其質點運動與分界面平行。以上兩種面波的速度都比體波小，但在地震記錄上，面波的振幅一般比體波大，原因之一是：體波是在三維中傳播，而面波則是二維的，所以體波位移隨距離的遞減率要比面波快。在離開震源一定距離後，地震記錄上的面波就比較顯著瞭。不過地震的面波成分和它的激發條件極有關系。大地震的面波總是很顯著的，但小地震的面波有時並不發育。

　　廣義瑞利波和洛夫波　瑞利波和洛夫波是面波中兩種基本類型。在成層的或速度隨深度變化的介質中，還可能存在其他類型的面波和導波；它們的傳播離不開界面，而是被界面所引導，在這些波中最重要的是所謂廣義的瑞利波和廣義的洛夫波。它們與以上的瑞利波和洛夫波不同之處在於它們的傳播速度是隨波的頻率（或波長）而變化。這個速度與頻率的關系曲線叫做頻散曲線。頻散曲線的意義在於它的形狀和地下巖石的成層結構和各層中的體波速度有關系。如果能在地面上測得各種頻率的瑞利波或洛夫波的傳播速度，就可以對地下的成層結構做出推斷。

　　地震波的運動學　地震波是傳播的運動，它所傳播的不是介質本身，而隻是介質的一種運動狀態。質點位移不大時，介質的運動方程是線性的，疊加原理可以應用，因此任一波動可用傅裡葉方法分解成簡諧波。關於波動的許多概念，如波長、頻率、周期、位相等等都是由簡諧波來的，這在計算上有些方便，但也不過是一種表示方法，並不意味著波動原來就是由簡諧波組成的。其實波動也可以分解成階梯函數或脈沖。為瞭具體，可將方程(2)或(3)寫成以下形式：

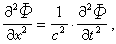
式中Φ是任一傳播的量，c是傳播速度。此式的簡諧波特解是

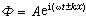的實部或虛部， A是常數，稱為振幅， ω和 k必須滿足 ω／ k= c。此式對於 x和 t 都是以 λ和 T為周期的周期函數，並有

ωT=kλ=2π，

λ稱為波長，T稱為周期，其倒數λ-1和T -1分別稱為波數和頻率，而k和ω各為波數和頻率的2π 倍，稱為圓周波數和圓周頻率。解

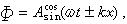
表示行波，“-”號的是前進波，“+”號的是後退波。由行波疊加，可得到駐波

。

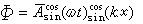大地震時可以激發地球自由振蕩。這原是駐波，但常做為相反方向傳播的行波的疊加來分析。取前進波

Φ=Acos(ωt-kx)，　　　　(6)

式中的ωt-kx =θ，稱為波的相位。一定的相位前進時，

Δθ=ωΔt-kΔx=0，

故

，

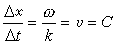v 稱為相速度。對於恒定的簡諧波(6)來說，相速度v 即等於傳播速度C，後者是波動方程的一個參數，是由介質的彈性和密度所確定的。此處需註意:式(6)表示一個恒定的一維無窮波列，它沒有起點和終點，而是全介質的一個穩定的運動狀態。但這隻是一個算學抽象。事實上，波動總是在某一時刻t0=0，某一地點x=0開始，經過

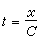時間才到達地點 x。在此以前，波動尚未發出或到達。所以正確的算學表達式應當是：

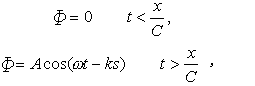(7)

這樣的運動稱為有因的，即是說，波動必須從某一個源出發，以一定的速度傳到點x；在波未到達之前，該點沒有波動。有因函數在波動分析中必須註意，否則會得到違反因果律的結果。對於式(7)，應用傅裡葉積分有困難，因為函數當t →∞時不收斂，但可以證明它可以用一個復平面上的積分來表示。

　　波速隨頻率或波長而變化，這種現象叫做頻散。在完全彈性的平行層介質中，由於各種類型的波的疊加，在地表面觀察到的面波速度隨頻率的變化是幾何原因造成的。在地球內部，由於介質的不均勻性和非完全彈性，也導致地震體波的頻散，這是物理原因造成的。由於頻散，波形在傳播過程中就會發生變化。例如在震源處發出的脈沖，在遠處就可散成一個波列。在一給定地點所觀測到的波動常常是許多波速和頻率略有差別的波疊加而成的，這就產生群速的現象。先取兩個振幅相同，而頻率和波數各相差小量Δω和Δk 的波的疊加為例：

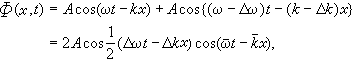
ϖ和k分別是平均頻率和波數。在上式中，振幅2ACOS

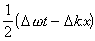也是向前傳播的，其速度是 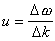，稱為群速度，它與相速度 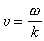一般是不同的。同樣的概念也可以推廣到許多波數相近的一群波的疊加。設這群波的波數包括在 K 0±∈范圍之內，∈是一小數。疊加後的波動是

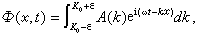
將位相改寫為：

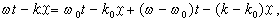
則立得

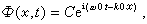
C是振幅函數，顯然以群速度

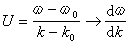
向前傳播。無頻散時，

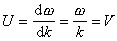，故群速度與相速度不分。有頻散時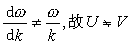， 。由定義， U又可寫為：

。

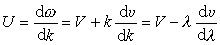　　以上的推導隻是根據波的運動學，但群速度的概念在動力學上也是有意義的，它其實就是波動能量的傳播速度。振幅函數C可寫為：

這是X-Ut的函數。對於線性的簡諧波動，平均能量密度Ē是和振幅的平方成比例的，故

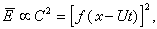
右端顯然是以群速度U傳播的，平均能量流應等於ĒU。

　　地震波的吸收和衰減　將地球介質看成是完全彈性體隻是一種幾近。精密的地震觀測表明，地震波的能量消耗有時是不能忽略的，而測量這種消耗也可以提供關於地球內部情況的更多信息。描述完全彈性體的胡克定律隻反映應力σ與應變e 的線性關系，不包含σ和e 的時間變化。但若有能量消耗時，它們的時間變化率@T(00752)和ė就需要考慮。實驗表明，若應變不超過10-5或10-6時，σ、e、@T(00752)、ė之間的關系仍是線性的，於是疊加原理仍可應用，這就大大簡化瞭計算。這樣的介質稱為線性固體。對於圓頻率為ω的簡諧波來說，

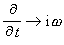。所以線性體的計算與完全彈性體相似，不過此時的彈性常數包括一個虛部而成為復數，其實部對應波的傳播，其虛部對應振幅的衰減。

　　能量的消耗可以用不同的方式來表示；測量的方法可以用振動，也可以用行波。振幅隨瞭時間的衰減可用

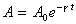表示，γ 稱為衰減系數。在一周期時間，兩個同方向振動幅度的比值的自然對數稱為對數減縮 Δ。故 Δ= γ T。對於行波，振幅因幾何擴散而減小，通常與震源距離的某次方成反比，但這與能量消耗無關。對於平面波，幾何擴散不必考慮。波傳播 x距離後，因介質對能量的吸收而導致振幅的減小，可用 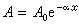表示， α稱為吸收系數。因能量與振幅的平方成比例，故能量的吸收系數為 2 α 。習慣上，衰減系數指的是時間變化，吸收系數指的是空間變化。對於後者，也同樣可采用對數減縮的概念，即定義 Δ′為相距一個波長的兩個振幅比值的自然對數，或 Δ′= αλ。 α 和 γ 都同頻率有關，在地震波的計算中，作為第一近似可假定它們與頻率成正比。

　　表示能量消耗的另一個重要參數Q叫做品質因子，這是由電路理論借用來的一個概念，定義是

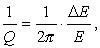(9)

E 是一定體積的介質在一周期時間內所存儲的最大應變能，ΔE是同時期所消耗的能量。在地球物理文獻中，近年來較普遍地采用Q值來說明地球介質的非完全彈性，因為它與頻率的依賴關系比α 或γ 弱得多。將以上定義應用於行波和駐波，可以證明：

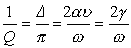， (10)

v 是波的傳播速度，ω是圓頻率。據此可見，對不同類型的波，Q值是不同的。例如P波和S波，非但它們的v不同，而且α 和γ也不同，因而相應的 Qp和Qs也不同。瑞利波包含縱波與橫波兩種成分，因而QR與Qp和Qs都有關系。對於一個泊松介質，即σ =0.25的介質，可以證明：

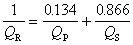。 (11)

　　由行波所測定的Q與由駐波所測定的Q略有不同。用駐波時，Δ是用相隔一周期的振幅比；用行波時，Δ′是用相隔一個波長的振幅比。若無頻散，λ=VT，V是相速度，則兩種測定的結果是相同的。若有頻散，則最大振幅的傳播速度應是群速度U而不是相速度V。使時間上的振幅衰減與空間上的振幅吸收相當，則應有

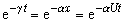。故γ＝ αU 。設由駐波和行波所測定的 Q值分別為 Qt和 Qx，則得 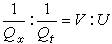。故有

VQx=UQt， 　　(12)

Q 值隨頻率的變化比吸收系數弱得多。在天然地震的頻率范圍內（約為10～0.01赫），Q值隨頻率的變化常是可以忽略的。

　　地震波的能量消失除由於介質的吸收外，還可由於波的散射。若介質中存在不均勻性，地震波通過時將發生不規則的反射和折射，向不同的方向傳播並彼此幹涉，最後化成熱能而消失或成為某種震動背景。這部分能量消耗也表現在振幅的衰減中，因而也影響Q值。

　　地震波的反射和折射　設有一平面波由介質1入射於介質2，其分界面為z=0。設波的傳播方向與xz面平行，波陣面法線的入射角為i。於是有

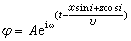，　　　　(13)

φ是波的位移，v 是傳播速度。若φ是P波，其位移方向與傳播方向平行，且v=vp；若φ是S波，則v=vs。但位移有兩個分量：一個平行於xz面並與傳播方向垂直，稱為SV；另一個則垂直於xz面，稱為SH。P與SV的位移因在同一平面內，故可疊加；SH的位移與傳播面垂直，可以獨立地計算。

　　當地震波入射到一個分界面時，若兩邊的介質不發生滑動，則計算時的邊界條件為：地震波所引起的位移和應力必須連續。當P波（或SV波）由介質1入射時，可以在介質2產生一對折射的P波和SV波，其折射角分別為i2和j2；並在介質1產生一對反射的P波和SV波，其反射角分別為 i2和j2。各折射與反射的波列可用與式(13)相似的公式來表示。應用以上運動在z=0時為連續的條件，立得

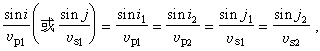(14)

其中腳標1、2各指相應的介質。此式稱為斯涅耳定律。根據邊界條件，還可計算折射波和反射波的振幅與入射波振幅之比，稱為透射系數和反射系數。它們一般比較復雜，但當界面是地表面時，結果是簡單的。因為地面可以幾近地看做是一個自由面，所以邊界條件簡化為：z=0時，應力分量等於零。當P波由地下入射到地面時，隻有兩個反射波（圖1）。由邊界條件可得

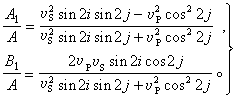　　　(15)

入射P波的入真射角為i，但由於反射SV波的存在，地面上所測得的視出射角θ不等於i，可以證明，

　　 　　θ=2j。由斯涅耳定律，可以解出真入射角i，

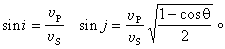
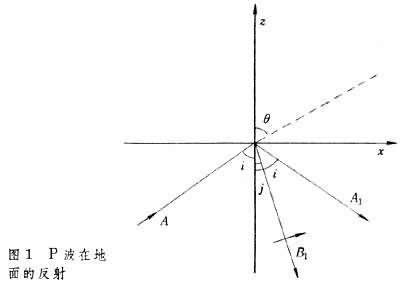
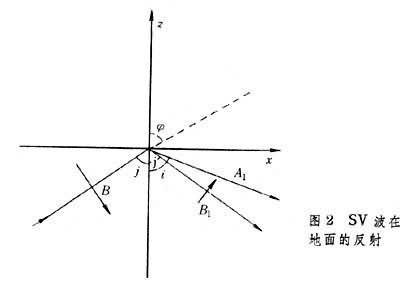
　　當SV波入射時（圖2），則有

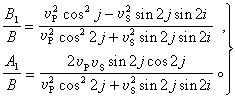　　(16)

對於橫波，位移方向與射線方向垂直，視出視角ϕ為：

，

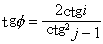由此可以解出真入射角j。

　　當SH波入射時，情況最簡單，反射波隻有一個SH波，其反射系數恒等於1。所以當SH波入射到地表面時，面上的位移振幅恒為入射振幅的兩倍。

　　地震射線　地震波的計算除在極簡單的幾何條件下，一般都是復雜的。在實際問題中，常常都是采用地震射線的概念，這和幾何光學很相似。所謂地震射線，就是地震波傳播時，波陣面法線的軌跡，也即是震動由一點傳播到另一點所經過的途徑。射線地震學，也叫幾何地震學，是波動地震學在波長很短時的近似。它可以由波動地震學推演出來，但更直接的是根據費馬原理。這個原理說：當一個震動由介質中一點傳播到另一點時，它所經過的途徑是使其傳播時間為一穩定值（最大、最小或拐點）。設震動由A點出發，沿途徑s傳播到B，傳播速度是v(x，у，z)，所用的時間是t，則費馬原理就是

。

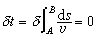δ是變分。根據這個原理，若A和B各在一個分界面的兩邊或一邊，就立刻得到斯涅耳的折射或反射定律。

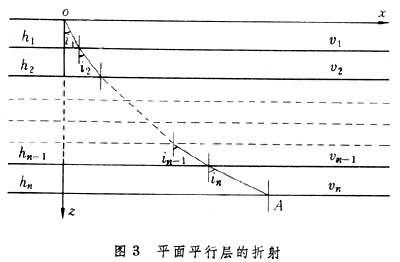
　　地面以下地震波傳播速度一般都是隨深度而增加的，因此地震射線總是向上彎曲。這就使得一條射線從震源出發，無論向何方向出射，最後總能彎回到地面。當地區不大時，地面的曲率可以忽略，地球介質可以看成是由平面平行層組成的。圖3表示這種情況，h 和v 各為層的厚度和其中的波速（為簡便計，隻考慮Vp，這對人工震源是合適的）。取x軸沿最上界面，z軸垂直向下。由0點至A點所需的傳播時間t為：

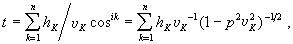(17)

其中 　

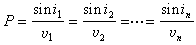為一常數。 A點的 x 坐標為：

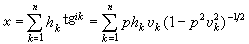。　(18)

若介質的性質是連續變化的，即v=v(z)，則可令hk→dz，n →∞，便得

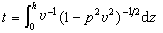，　　　(17a)

。　　(18a)

若v =v(z)為已知，則上式可以求出。由圖3可見，折射波在A點反射而又回到地面。若A點的in為90°，則可不經反射而全程都是折射波，以A點為射線途徑的最低點。

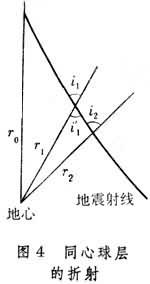
　　研究大區域時，地面曲率不能忽略。此時地球可看成是同心層組成的。由圖4可見

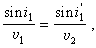但

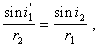
故

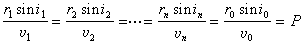
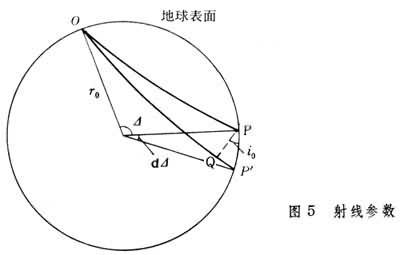
是一常數，r0是地球半徑，v0是地面附近的波速。對於一給定的射線，p是不變的，其值取決於射線離開地面時的出射角i0，叫做射線參數。它與地面上量得的走時（即t-Δ關系）有一簡單關系。由圖5，設相鄰兩點P和P′的震中距離各為Δ及Δ+dΔ。作PQ垂直於射線OP。PP′=r0dΔ，P′Q=v0dt，由此可得

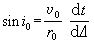。故 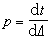。若 t- Δ關系為已知，則 p可以求得，它與 △有一定的關系。

　　在球對稱的情況下，與平面關系式(17)、(18)式相對應的公式是

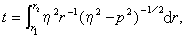　　(19)

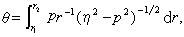　　　(20)

式中η=r/v，θ是射線上兩點在地心所張的角，r1和r2是兩點的向徑。設一射線由地面附近出射，連續折射後又在震中距離△處回到地面。設其途徑的最低點的r。在式(20)中，取r1=r =Pv，r2=r0，θ=△/2，得

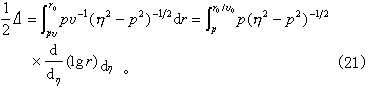
上式左端是p的已知函數，右端lgr是η的待定函數。這是一個阿貝型的積分方程，其解是已知的，可寫為：

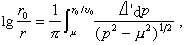　 (22)

μ是p的最低值 (μ=r/v)，即震中距離為△的射線參數。上式給出r與r/v的關系，也即是v與r的關系（△′是相當於任何 p的△值）。如果地下波速隨深度的變化是連續的並滿足一定的限制條件，式(22)可以使人們從地面的地震波走時的觀測，計算出地下波速隨深度的分佈。這是射線理論最偉大的成就。為瞭便於計算，可應用以下變換：設△′為小於△的一個震中距離，並令

，

代入上式，化簡，得

，

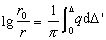此式可根據走時表求數值積分。由v =r/μ可求得v。

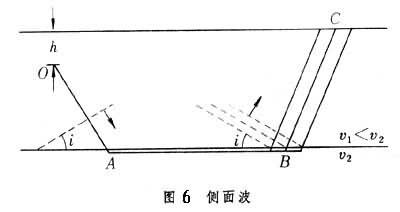
　　若介質是分層的，當地震波由低速的一方向高速的一方入射時，還存在一種波，叫做側面波（或叫首波、折射波、衍射波、行走反射波，等等），這在光波中不易見到，但在地震波中則為常見。這種波以臨界角(i=arc sinv1/v2)入射後，又以臨界角連續出射。若在地下深為h處有一震源，則在一定的震中距離之處的任一點C都可觀測到這種側面波。射線OABC是滿足費馬原理的，但AB射線如何又能折回則是射線理論所不能解釋的，必須從波動方程中求得答案。但它的存在也可以簡單地給與定性的說明。震動沿AB路徑的傳播速度是v2，但這是沿分界面傳播的，所以也必影響介質1。因v2大於介質1中的固有速度v1，按照惠更斯原理，在介質1中就產生一種首波，如同子彈在空氣中以超音速飛行相似，但這個波在介質2中並不存在，所以隻是一個半首波。在多層介質中，可以存在來自不同界面的側面波。在地震勘探或地震測深的工作中所用的折射法，其實就是根據側面波，而不是真正的折射波。

　　

參考書目

　佈倫著，朱傳鎮、李欽祖譯：《地震學引論》，科學出版社，北京，1965。(K.E.Bullen，An Introduction to the Theory of Seismology，3rd edition，Cambridge Univ.Press，London，1963.)

　傅承義、陳運泰、祁貴仲：《地球物理學基礎》，科學出版社，北京，1985。