向量概念的推廣。設V是n維向量空間,V上全體線性函數的集合L(V;R)也是一個n維向量空間,稱為V的對偶空間,記為V *。反過來,V也可以看作V *的對偶空間,即V=(V *)*=L(V *;R)。設V有一個基底變換
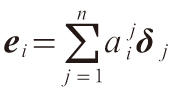 ,則
V中元素
x的兩組分量(
x
1,…,
x
n)和
,則
V中元素
x的兩組分量(
x
1,…,
x
n)和
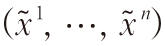 ,即:
,即:
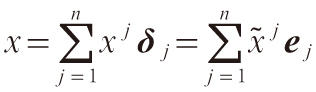 滿足關系式:
滿足關系式:
 或
或
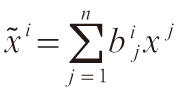 其中
其中
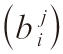 是
是
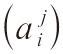 的逆矩陣。但是
V
*中元素
α的分量
α
i=
α(
δ
i)和
的逆矩陣。但是
V
*中元素
α的分量
α
i=
α(
δ
i)和
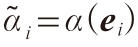 的變換規律是:
的變換規律是:
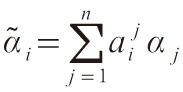 把
V
*中的元素稱為
V上的
協變向量,或
一階協變張量,把
V本身的元素稱為
V上的
反變向量,或
一階反變張量。
把
V
*中的元素稱為
V上的
協變向量,或
一階協變張量,把
V本身的元素稱為
V上的
反變向量,或
一階反變張量。
一般地,V上r重線性函數
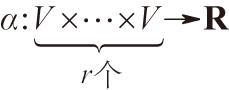 稱為
V上的
r階協變張量,
V
*上的
s重線性函數
稱為
V上的
r階協變張量,
V
*上的
s重線性函數
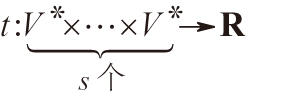 稱為
V上的
s階反變張量。若
f是
p階反變、
q階協變的張量,即:
稱為
V上的
s階反變張量。若
f是
p階反變、
q階協變的張量,即:
 則稱
f是
(p,q)型張量。
則稱
f是
(p,q)型張量。
在力學和數學中有許多量在坐標系下表示為一組數(稱為分量),當坐標變換時,分量按照一定的變換規則進行變換,如前面提到的V中的元素和V上的線性函數。在歷史上,張量是用分量的變換規律來定義的。具體地說,所謂的一個(p,q)型張量(即p階反變、q階協變的張量)T是指n維向量空間V的每一個基底{δi}都對應著一組np+q個數:
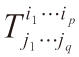 ,
i
1,…,
ip,
j
1,…,
jq=1,2,…,
n當基底變換時,設:
,
i
1,…,
ip,
j
1,…,
jq=1,2,…,
n當基底變換時,設:
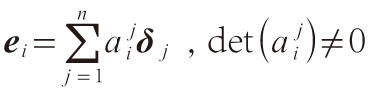 則對應的數組
則對應的數組
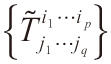 滿足關系式:
滿足關系式:
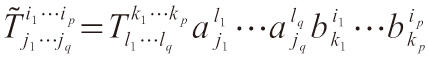 其中采用瞭愛因斯坦的和式約定(重復出現的指標表示求和),且(
b ij)是(
a
i
j)的逆矩陣。上面兩種定義是一致的。
其中采用瞭愛因斯坦的和式約定(重復出現的指標表示求和),且(
b ij)是(
a
i
j)的逆矩陣。上面兩種定義是一致的。
(p,q)型張量的集合:
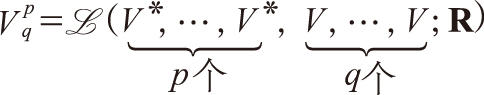 是
n
p+q維向量空間,有加法、數乘法和張量積運算。在黎曼幾何出現之後,
G.裡奇和
T.列維–齊維塔系統地發展瞭張量分析和絕對微分學,定義瞭張量場的絕對微分。後來,逐步發展成現在所稱的
聯絡。
是
n
p+q維向量空間,有加法、數乘法和張量積運算。在黎曼幾何出現之後,
G.裡奇和
T.列維–齊維塔系統地發展瞭張量分析和絕對微分學,定義瞭張量場的絕對微分。後來,逐步發展成現在所稱的
聯絡。
張量的概念在力學、物理學和數學中有廣泛的應用。例如,黎曼度量就是光滑流形上的一個對稱的、正定的二階協變張量,在局部坐標系(xi)下,它可表示為:
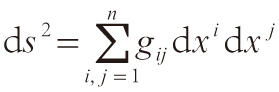 復流形上的復結構是滿足條件
復流形上的復結構是滿足條件
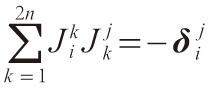 的(1,1)型張量場
的(1,1)型張量場
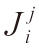 。
辛流形上的辛結構是光滑流形上的一個非退化的二階協變的反對稱張量場,在局部坐標系(
x
i)下,它可表示為:
。
辛流形上的辛結構是光滑流形上的一個非退化的二階協變的反對稱張量場,在局部坐標系(
x
i)下,它可表示為:
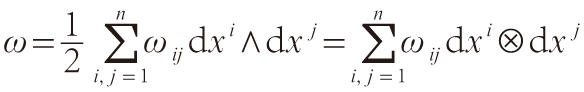 式中
ω
ij=−
ω
ji,det(
ω
ij)≠0。
式中
ω
ij=−
ω
ji,det(
ω
ij)≠0。